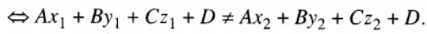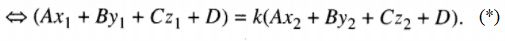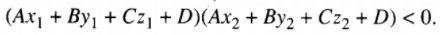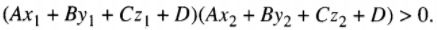Bài 52 trang 127 Sách bài tập Hình học lớp 12 Nâng caoTrong không gian Oxyz cho hai điểm
Lựa chọn câu để xem lời giải nhanh hơn
Trong không gian Oxyz cho hai điểm \({M_1}({x_1};{y_1};{z_1}),{M_2}({x_2};{y_2};{z_2})\) không nằm trên mặt phẳng \(\left( \alpha \right):Ax + By + Cz + D = 0.\) Tìm điều kiện cần và đủ để : LG a Đường thẳng \({M_1}{M_2}\) cắt \(\left( \alpha \right)\) Lời giải chi tiết: Đường thẳng \({M_1}{M_2}\) cắt \(\left( \alpha \right)\) khi và chỉ khi \(\overrightarrow {{M_1}{M_2}} \) không vuông góc với \(\overrightarrow n \left( {A,B,C} \right)\) \(\overrightarrow n \) là vec tơ pháp tuyến của \(\left( \alpha \right)\), tức là : \(\eqalign{ & \overrightarrow {{M_1}{M_2}} .\overrightarrow n = 0\cr& \Leftrightarrow A({x_2} - {x_1}) + B({y_2} - {y_1}) + C({z_2} - {z_1}) \ne 0 \cr} \)
LG b Đoạn thẳng \({M_1}{M_2}\) cắt \(\left( \alpha \right)\) Lời giải chi tiết: Đoạn thẳng \({M_1}{M_2}\) cắt \(\left( \alpha \right)\) khi và chỉ khi có một điểm I thuộc\(\left( \alpha \right)\) và chia đoạn thẳng \({M_1}{M_2}\) theo một tỉ số k<0. Gọi \(\left( {{x_0};{y_0};{z_0}} \right)\) là tọa độ của điểm I, ta có : \({x_0} = {{{x_1} - k{x_2}} \over {1 - k}},{x_0} = {{{y_1} - k{y_2}} \over {1 - k}},{x_0} = {{{z_1} - k{z_2}} \over {1 - k}}\) Và \(A{x_0} + B{y_0} + C{z_0} + D = 0\). \( \Rightarrow A\left( {{{{x_1} - k{x_2}} \over {1 - k}}} \right) + B\left( {{{{y_1} - k{y_2}} \over {1 - k}}} \right) + C\left( {{{{z_1} - k{z_2}} \over {1 - k}}} \right) + D = 0\)
Vì k < 0 nên điều kiện trên tương đương với điều kiện
LG c Đường thẳng \({M_1}{M_2}\) cắt \(\left( \alpha \right)\) tại I sao cho M1 nằm giữa I và M2 Lời giải chi tiết: \({M_1}\) nằm giữa I và \({M_2}\) \( \Leftrightarrow I\) chia đoạn \({M_1}{M_2}\) theo tỉ số k mà 0< k <1. Ta vẫn có điều kiện \(\left( * \right)\), nhưng vì 0< k \(0 < {{A{x_1} + B{y_1} + C{z_1} + D} \over {A{x_2} + B{y_2} + C{z_2} + D}} < 1.\) LG d Đường thẳng \({M_1}{M_2}\) cắt \(\left( \alpha \right)\) tại I sao cho M2 nằm giữa I và M1. Lời giải chi tiết: Tương tự như trên, ta có điều kiện : \(0 < {{A{x_2} + B{y_2} + C{z_2} + D} \over {A{x_1} + B{y_1} + C{z_1} + D}} < 1.\) Chú ý : Từ kết quả trên ta suy ra kết luận sau: Hai điểm \({M_1}({x_1};{y_1};{z_1})\) và \({M_2}({x_2};{y_2};{z_2})\) nằm cùng một phía đối với mặt phẳng \(\left( \alpha \right):Ax + By + Cz + D = 0.\) khi và chỉ khi
HocTot.Nam.Name.Vn
|