Bài 49 trang 126 Sách bài tập Hình học lớp 12 Nâng caoCho hình hộp chữ nhật ABCD.A’B’C’D’
Lựa chọn câu để xem lời giải nhanh hơn
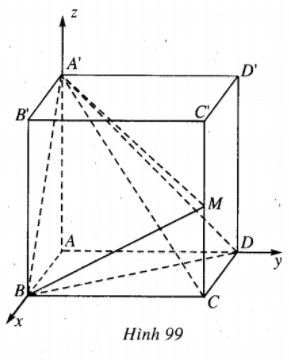
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có A(0;0;0), B(a;0;0), D(0;a;0), A’(0;0;b) với a, b là những số dương và M là trung điểm của CC’. LG a Tính thể tích của tứ diện BDA’M. Lời giải chi tiết:
Từ giả thiết ta có C=(a;a;0). \(C' = (a;a;b) \Rightarrow M = \left( {a;a;{b \over 2}} \right)\) Ta có \(\overrightarrow {BD} = \left( { - a;a;0} \right);\) \(\overrightarrow {BM} = \left( {0;a;{b \over 2}} \right);\,\,\overrightarrow {BA'} = \left( { - a;0;b} \right)\) \( \Rightarrow \left( {\left[ {\overrightarrow {BD} ,\overrightarrow {BM} } \right]} \right) = \left( {{{ab} \over 2};{{ab} \over 2}; - {a^2}} \right)\) Vậy \({V_{BDA'M}} = {1 \over 6}\left| {\left[ {\overrightarrow {BD} ,\overrightarrow {BM} } \right].\overrightarrow {BA'} } \right| = {{{a^2}b} \over 4}.\) LG b Tìm tỉ số \({a \over b}\) để mp(A’BD) vuông góc với mp(MBD). Lời giải chi tiết: Mặt phẳng (A’BD) có vec tơ pháp tuyến \(\overrightarrow {{n_1}} = \left[ {\overrightarrow {BD} ,\overrightarrow {BA'} } \right] = (ab;ab;{a^2}).\) Mặt phẳng (MBD) có vectơ pháp tuyến \(\overrightarrow {{n_2}} = \left[ {\overrightarrow {BD} ,\overrightarrow {BM} } \right] = ({{ab} \over 2};{{ab} \over 2}; - {a^2}).\) Vì vậy \(\eqalign{ & \left( {MBD} \right) \bot (A'BD) \Leftrightarrow \overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 0 \cr & \Leftrightarrow {{{a^2}{b^2}} \over 2} + {{{a^2}{b^2}} \over 2} - {a^4} = 0 \cr & \Leftrightarrow {a^2}{b^2} = {a^4} \Leftrightarrow {a^2} = {b^2} \Leftrightarrow a = b \Leftrightarrow {a \over b} = 1. \cr & \cr} \) (do \(a > 0,b > 0).\) HocTot.Nam.Name.Vn
|