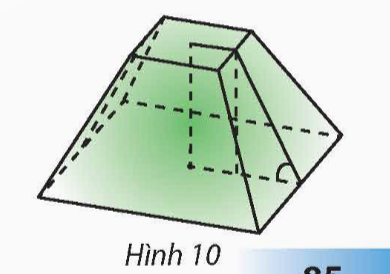
Toán 11, giải toán lớp 11 chân trời sáng tạo

Bài 5 trang 85 SGK Toán 11 tập 2 – Chân trời sáng tạo

Người ta định đào một cái hầm có dạng hình chóp cụt tứ giác đều có hai cạnh đáy là 14 m và 10 m.

Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Lí - Hóa - Sinh

Đề bài

Người ta định đào một cái hầm có dạng hình chóp cụt tứ giác đều có hai cạnh đáy là 14 m và 10 m. Mặt bên tạo với đáy nhỏ thành một góc nhị diện có số đo bằng 135°. Tính số mét khối đất cần phải di chuyển ra khỏi hầm.

Phương pháp giải - Xem chi tiết

‒ Cách xác định góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\)

Bước 1: Xác định \(c = \left( {{P_1}} \right) \cap \left( {{Q_1}} \right)\).

Bước 2: Tìm mặt phẳng \(\left( R \right) \supset c\).

Bước 3: Tìm \(p = \left( R \right) \cap \left( {{P_1}} \right),q = \left( R \right) \cap \left( {{Q_1}} \right),O = p \cap q,M \in p,N \in q\).

Khi đó \(\left[ {{P_1},d,{Q_1}} \right] = \widehat {MON}\).

‒ Sử dụng công thức tính thể tích khối chóp cụt đều: \(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right)\).

Lời giải chi tiết

Mô hình hoá cái hầm bằng cụt chóp tứ giác đều \(ABCD.A'B'C'D'\) với \(O,O'\) là tâm của hai đáy. Vậy \(AB = 14,A'B' = 10\).

Gọi \(M,M'\) lần lượt là trung điểm của \(CD,C'D'\).

\(A'B'C'{\rm{D}}'\) là hình vuông \( \Rightarrow O'M' \bot C'{\rm{D}}'\)

\(CDD'C'\) là hình thang cân \( \Rightarrow MM' \bot C'D'\)

Vậy \(\widehat {MM'O'}\) là góc nhị diện giữa mặt bên và đáy nhỏ.

\( \Rightarrow \widehat {MM'O'} = {135^ \circ } \Rightarrow \widehat {M'MO} = {180^ \circ } - \widehat {MM'O'} = {45^ \circ }\)

Kẻ \(M'H \bot OM\left( {H \in OM} \right)\)

\(OMM'O'\) là hình chữ nhật

\( \Rightarrow OH = O'M' = 5,MH = OM - OH = 2,M'H = OO' = MH.\tan {45^ \circ } = 2\)

Diện tích đáy lớn là: \(S = A{B^2} = {14^2} = 196\left( {{m^2}} \right)\)

Diện tích đáy bé là: \(S' = A'B{'^2} = {10^2} = 100\left( {{m^2}} \right)\)

Số mét khối đất cần phải di chuyển ra khỏi hầm là:

\(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right) = \frac{1}{3}.2\left( {196 + \sqrt {196.100} + 100} \right) = \frac{{872}}{3} \approx 290,67\left( {{m^3}} \right)\)

Chia sẻ