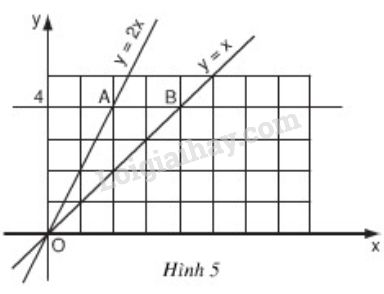
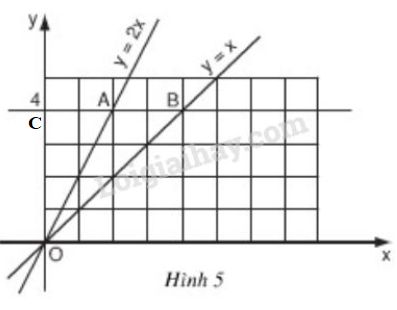
Bài 5 trang 45 SGK Toán 9 tập 1

Đề bài

a) Vẽ đồ thị hàm số $y = x$ và $y =2x$ trên cùng một mặt phẳng tọa độ $Oxy$  $(h.5)$.

b) Đường thẳng song song với trục $Ox$ và cắt trục $Oy$ tại điểm có tung độ $y = 4$ lần lượt cắt các đường thẳng $y = 2x,\ y = x$ tại hai điểm $A$ và $B$.

Tìm tọa độ của các điểm $A,\ B$ và tính chu vi, diện tích của tam giác $OAB$ theo đơn vị đo trên các trục tọa độ là xentimét.

Lời giải chi tiết

a) Xem hình trên và vẽ lại 

b)

+) Ta coi mỗi ô vuông trên hình $5$ là một hình vuông có cạnh là $1cm$.

    Từ hình vẽ ta xác định được: $A(2; 4),\ B(4; 4)$.

+) Tính độ dài các cạnh của $∆OAB$:

Dễ thấy $AB = 4 - 2 = 2$  $(cm)$.

Gọi $C$ là điểm nằm trên trục tung, có tung độ là $4$, ta có $OC=4cm,AC=2cm;BC=4cm$

Áp dụng định lý Py-ta-go cho các tam giác vuông $OAC$ và $OBC$, ta có:

$\eqalign{ & OA = \sqrt {{AC^2} + {OC^2}} = \sqrt {{2^2} + {4^2}} = 2\sqrt 5 \left( {cm} \right) \cr & OB = \sqrt {{BC^2} + {OC^2}}= \sqrt {{4^2} + {4^2}} = 4\sqrt 2 \left( {cm} \right) \cr}$

$\Rightarrow$ Chu vi $\Delta OAB$ là:

$C_{\Delta OAB}=OA + OB + AB$

              $=2+ 2\sqrt 5 + 4\sqrt 2  \approx  12,13(cm)$

+) Tính diện tích $∆OAB$:

Cách 1:

$\eqalign{ & {S_{\Delta OAB}} = {S_{\Delta OBC}} - {S_{\Delta OAC}} \cr & = {1 \over 2}OC.BC - {1 \over 2}OC.AC \cr & = {1 \over 2}{.4^2} - {1 \over 2}.4.2 = 8 - 4 = 4\left( {c{m^2}} \right) \cr}$

Cách 2: 

$∆OAB$ có đường cao ứng với cạnh $AB$ là $OC$.

$\Rightarrow S_{∆OAB}=\dfrac{1}{2}.OC.AB=\dfrac{1}{2}.4.2=4$ $(cm^2)$

HocTot.Nam.Name.Vn