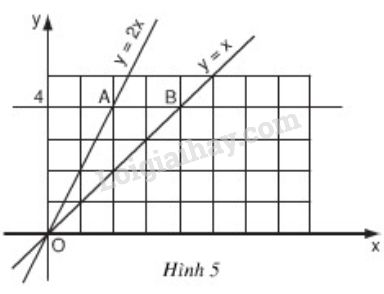
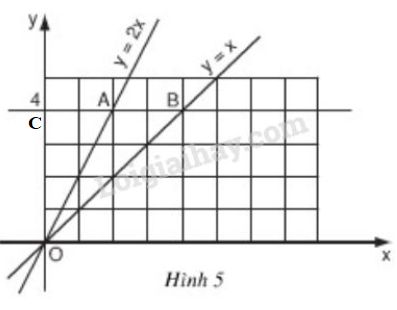
Bài 5 trang 45 SGK Toán 9 tập 1Vẽ đồ thị hàm số y = x Đề bài a) Vẽ đồ thị hàm số y=xy=x và y=2xy=2x trên cùng một mặt phẳng tọa độ OxyOxy (h.5)(h.5). b) Đường thẳng song song với trục OxOx và cắt trục OyOy tại điểm có tung độ y=4y=4 lần lượt cắt các đường thẳng y=2x, y=xy=2x, y=x tại hai điểm AA và BB. Tìm tọa độ của các điểm A, BA, B và tính chu vi, diện tích của tam giác OABOAB theo đơn vị đo trên các trục tọa độ là xentimét.
Video hướng dẫn giải Phương pháp giải - Xem chi tiết a) Cách vẽ đồ thị hàm số y=ax, (a≠0)y=ax, (a≠0): Cho x=x0⇒y0=ax0x=x0⇒y0=ax0 Đồ thị hàm số y=ax(a≠0)y=ax(a≠0) là đường thẳng đi qua gốc tọa độ và điểm A(x0;y0)A(x0;y0) b) +) Đường thẳng song song với trục OxOx cắt trục OyOy tại điểm có tung độ y=by=b có phương trình đường thẳng là y=b.y=b. +) Muốn tìm tọa độ giao điểm của hai đường thẳng y=axy=ax và y=a′x ta giải phương trình ax=a′x tìm được hoành độ. Thay hoành độ vào một trong hai đường thẳng trên tìm được tung độ. +) Sử dụng đinh lí Py - ta - go trong tam giác vuông: ΔABC vuông tại A thì AB2+AC2=BC2. +) Chu vi tam giác: C∆OAB=AB+BO+AO. +) Diện tích ΔABC có đường cao h và a là độ dài cạnh ứng với đường cao: S∆OAB=12.h.a Lời giải chi tiết a) Xem hình trên và vẽ lại
b) +) Ta coi mỗi ô vuông trên hình 5 là một hình vuông có cạnh là 1cm. Từ hình vẽ ta xác định được: A(2;4), B(4;4). +) Tính độ dài các cạnh của ∆OAB: Dễ thấy AB=4−2=2 (cm). Gọi C là điểm nằm trên trục tung, có tung độ là 4, ta có OC=4cm,AC=2cm;BC=4cm Áp dụng định lý Py-ta-go cho các tam giác vuông OAC và OBC, ta có: OA=√AC2+OC2=√22+42=2√5(cm)OB=√BC2+OC2=√42+42=4√2(cm) ⇒ Chu vi ΔOAB là: CΔOAB=OA+OB+AB =2+2√5+4√2≈12,13(cm) +) Tính diện tích ∆OAB: Cách 1: SΔOAB=SΔOBC−SΔOAC=12OC.BC−12OC.AC=12.42−12.4.2=8−4=4(cm2) Cách 2: ∆OAB có đường cao ứng với cạnh AB là OC. ⇒S∆OAB=12.OC.AB=12.4.2=4 (cm2) HocTot.Nam.Name.Vn
|