Bài 5 trang 223 Sách bài tập Hình học lớp 12 Nâng cao.Cho khối lăng trụ tam giác đều ABC.A'B'C'
Lựa chọn câu để xem lời giải nhanh hơn
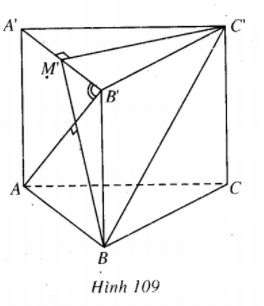
Cho khối lăng trụ tam giác đều ABC.A'B'C' có chiều cao bằng h và hai đường thẳng AB' và BC vuông góc với nhau. LG a Gọi M' là trung điểm của A'B'. Chứng minh rằng \(AB' \bot BM'.\) Lời giải chi tiết: (h.109)
Ta có C'M' \( \bot \) A'B, C'M' \( \bot \) AA' => C'M' \( \bot \) (ABB'A') => C'M' \( \bot \) AB. Mặt khác, theo giả thiết BC' \( \bot \) AB', suy ra AB' \( \bot \) mp(BC'M'). Do đó AB' \( \bot \) BM'. LG b Tính độ dài đoạn thẳng A'B' theo h. Lời giải chi tiết: Từ kết quả của câu a), ta dễ dàng suy ra \(\Delta BB'M'\) đồng dạng \( \Delta B'A'A\) \(\eqalign{ & \Rightarrow {{A'B'} \over {BB'}} = {{A'A} \over {B'M'}} \cr & \Rightarrow A'B'.B'M' = A'A.BB' \cr & \Rightarrow {1 \over 2}A'B{'^2} = {h^2} \cr & \Rightarrow A'B' = h\sqrt 2 . \cr} \) LG c Tính thể tích khối lăng trụ đã cho. Lời giải chi tiết: \({V_{ABC.A'B'C'}} = {S_{A'B'C'}}.AA'\) \(= {\left( {h\sqrt 2 } \right)^2}.{{\sqrt 3 } \over 4}h = {{\sqrt 3 } \over 2}{h^3}.\) HocTot.Nam.Name.Vn
|