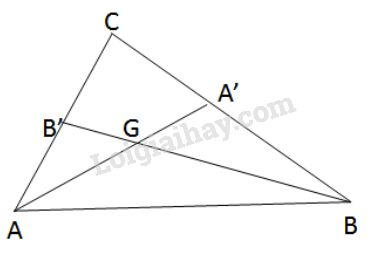
Bài 5 trang 132 SGK Toán 8 tập 2

Đề bài

Trong tam giác $ABC$ các đường trung tuyến $AA’$ và $BB’$ cắt nhau ở $G$. Tính diện tích tam giác $ABC$ biết rằng diện tích tam giác $ABG$ bằng $S.$

Lời giải chi tiết

 

Ta có: $AC = 2AB’$ (tính chất trung tuyến)

Mà $\Delta ABC,\,\Delta ABB'$ có cùng chiều cao hạ từ đỉnh $B$ xuống đáy $AC$.

$\Rightarrow$ ${S_{ABC}} = 2{S_{ABB'}}$ (1)

Xét $\Delta ABC$ có các đường trung tuyến $AA’$ và $BB’$ cắt nhau ở $G$ (gt)

$\Rightarrow$ $G$ là trọng tâm của $\Delta ABC$ (định nghĩa trọng tâm)

$\Rightarrow$ $BB' = \dfrac{3}{2}BG$ (tính chất trọng tâm) 

Suy ra chiều cao hạ từ $B'$ xuống đáy $AB$ bằng $\dfrac{3}{2}$ lần chiều cao hạ từ $G$ xuống đáy $AB$

Mà $\Delta ABG,\,\Delta ABB'$ chung đáy $AB$

Nên ${S_{ABB'}} = \dfrac{3}{2}{S_{ABG}}$ (2)

Từ (1), (2) suy ra ${S_{ABC}} = 2.\dfrac{3}{2}{S_{ABG}} = 3S$

HocTot.Nam.Name.Vn