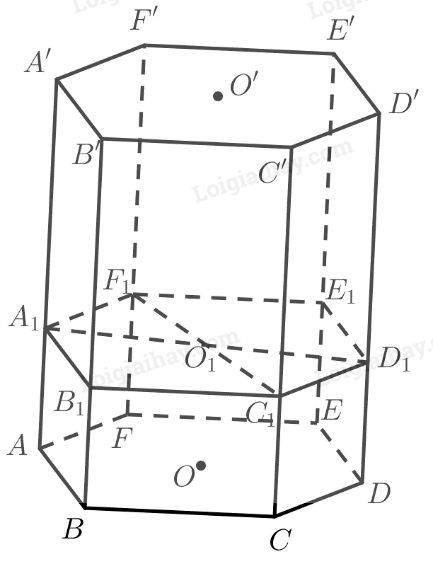
Bài 5 trang 120 SGK Toán 11 tập 1 - Chân trời sáng tạoĐể làm một khung lồng đèn kéo quân hình lăng trụ lục giác\(ABCDEF.A'B'C'D'E'F'\), Bình gắn hai thanh tre \({A_1}{D_1},{F_1}{C_1}\) song song với mặt phẳng đáy và cắt nhau tại \({O_1}\) (Hình 19). Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh Đề bài Để làm một khung lồng đèn kéo quân hình lăng trụ lục giác\(ABCDEF.A'B'C'D'E'F'\), Bình gắn hai thanh tre \({A_1}{D_1},{F_1}{C_1}\) song song với mặt phẳng đáy và cắt nhau tại \({O_1}\) (Hình 19). a) Xác định giao tuyến của \(mp\left( {{A_1}{D_1},{F_1}{C_1}} \right)\) với các mặt bên của lăng trụ. b) Cho biết \(A'{A_1} = 6A{A_1}\) và \(AA' = 70{\rm{ }}cm\). Tính \(C{C_1}\) và \({C_1}C'\).
Phương pháp giải - Xem chi tiết ‒ Để tìm giao tuyến của hai mặt phẳng, ta có 2 cách: + Cách 1: Tìm 2 điểm chung phân biệt. Giao tuyến là đường thẳng đi qua hai điểm chung. + Cách 2: Tìm 1 điểm chung và 2 đường thẳng song song nằm trên mỗi mặt phẳng. Giao tuyến là đường thẳng đi qua điểm chung và song song với hai đường thẳng đó. ‒ Sử dụng định lí Thalès. Lời giải chi tiết
a) Gọi \({B_1},{E_1}\) lần lượt là giao điểm của \(mp\left( {{A_1}{D_1},{F_1}{C_1}} \right)\) với \(BB',EE'\). Ta có: \(\left. \begin{array}{l}{A_1}{D_1}\parallel \left( {ABC{\rm{DEF}}} \right)\\{F_1}{C_1}\parallel \left( {ABC{\rm{DEF}}} \right)\\{A_1}{D_1},{F_1}{C_1} \subset mp\left( {{A_1}{D_1},{F_1}{C_1}} \right)\end{array} \right\} \Rightarrow mp\left( {{A_1}{D_1},{F_1}{C_1}} \right)\parallel \left( {ABC{\rm{DEF}}} \right)\) Vậy giao tuyến của \(mp\left( {{A_1}{D_1},{F_1}{C_1}} \right)\) với các mặt bên của lăng trụ là: \(\begin{array}{l}mp\left( {{A_1}{D_1},{F_1}{C_1}} \right) \cap \left( {ABB'A'} \right) = {A_1}{B_1}\\mp\left( {{A_1}{D_1},{F_1}{C_1}} \right) \cap \left( {BCC'B'} \right) = {B_1}{C_1}\\mp\left( {{A_1}{D_1},{F_1}{C_1}} \right) \cap \left( {C{\rm{DD'C'}}} \right) = {C_1}{D_1}\\mp\left( {{A_1}{D_1},{F_1}{C_1}} \right) \cap \left( {DEE'D'} \right) = {D_1}{E_1}\\mp\left( {{A_1}{D_1},{F_1}{C_1}} \right) \cap \left( {EFF'E'} \right) = {E_1}{F_1}\\mp\left( {{A_1}{D_1},{F_1}{C_1}} \right) \cap \left( {AFF'A'} \right) = {A_1}{F_1}\end{array}\) b) \(ABCDEF.A'B'C'D'E'F'\) là hình lăng trụ \( \Rightarrow CC' = AA' = 70\left( {cm} \right)\) \(A'{A_1} = 6A{A_1} \Rightarrow A{A_1} = \frac{1}{7}AA' = 10\left( {cm} \right)\) \(mp\left( {{A_1}{D_1},{F_1}{C_1}} \right)\parallel \left( {ABC{\rm{DEF}}} \right)\parallel \left( {A'B'C'{\rm{D'E'F'}}} \right)\) \(\begin{array}{l} \Rightarrow \frac{{C{C_1}}}{{CC'}} = \frac{{A{A_1}}}{{AA'}} \Leftrightarrow C{C_1} = \frac{{CC'.A{A_1}}}{{AA'}} = \frac{{70.10}}{{70}} = 10\left( {cm} \right)\\ \Rightarrow {C_1}C' = CC' - C{C_1} = 70 - 10 = 60\left( {cm} \right)\end{array}\)
|