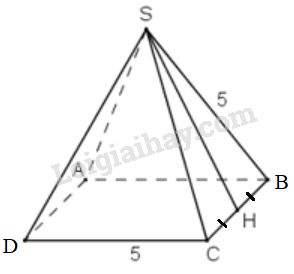
Bài 48 trang 125 SGK Toán 8 tập 2

LG a.

Hình chóp tứ giác đều, biết cạnh đáy \(a = 5cm\), cạnh bên \(b = 5cm,\;\sqrt{18,75}\approx 4,33 \) 

Phương pháp giải:

Áp dụng các công thức : 

\(S_{tp} = S_{xq} +S{đ}\) 

\(S_{xq} = p.d \), trong đó \(p \) là nửa chu vi đáy, \( d\) là trung đoạn của hình chóp.

Giải chi tiết:

Từ đề bài ta có các mặt bên của hình chóp đều là những tam giác đều cạnh \(5cm\).

Đường cao của mỗi mặt bên là: 

 \(d=SH = \sqrt{SC^{2} -HC^{2}}\)

 \(= \sqrt{5^{2} -2,5^{2}}= \sqrt{18,75}\approx 4,33 (cm) \)

Diện tích xung quanh hình chóp là:

        \(S_{xq} = p.d = \dfrac{1}{2}. 5.4.4,33 = 43,3 (cm^2) \) 

Diện tích đáy hình chóp:

        \(S_{đ} = a^2 = 5^2 =25(cm^2) \)

Diện tích toàn phần hình chóp:

        \( S_{tp} = S_{xq}+ S_{đ} = 43,3 + 25 = 68,3 \) \((cm^2)\)

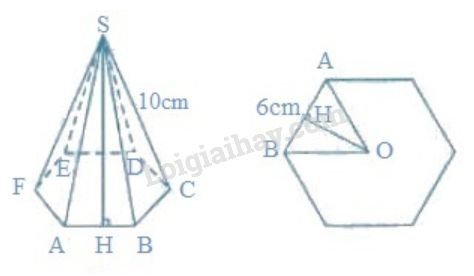
LG b.

Hình chóp lục giác đều, biết cạnh đáy \(a = 6cm\), cạnh bên \(b = 10cm,\; \sqrt{3}\approx 1,73; \;\sqrt{91}\approx 9,54\)

Phương pháp giải:

Áp dụng các công thức :

\(S_{tp} = S_{xq} +S{đ}\) 

\(S_{xq} = p.d \), trong đó \(p \) là nửa chu vi đáy, \( d\) là trung đoạn của hình chóp.

Giải chi tiết:

Mặt bên của hình chóp lục giác đều là tam giác cân có cạnh bên \(10cm\), cạnh đáy \(6cm\) .

Đường cao \(SH\) của mặt bên là: 

  \(d=SH = \sqrt{SA^{2} -AH^{2}} = \sqrt{10^{2} -3^{2}} \) \(= \sqrt{91}\approx   9,54 (cm) \) 

Diện tích xung quanh hình chóp:

       \(S_{xq} = p.d = \dfrac{1}{2}. 6.6.9,54 = 171,72\) \( (cm^2) \) 

Đáy của hình chóp là lục giác đều. Diện tích lục giác bằng \(6\) lần diện tích tam giác đều \(ABO\).

Chiều cao của tam giác đều OAB là:

 \(OH = \sqrt{OB^{2} -BH^{2}} = \sqrt{6^{2} -3^{2}}\) \(= \sqrt{27}\approx  5,2 (cm) \) 

Diện tích đáy hình chóp:

        \(S_{đ} =6.\dfrac{1}{2}.OH.AB=6. \dfrac{1}{2}5,2.6 = 93,6(cm^2) \)

Diện tích toàn phần hình chóp: 

        \( S_{tp} = S_{xq}+ S_{đ} = 171,72 + 93,6 \) \(= 265,32 (cm^2)\)

HocTot.Nam.Name.Vn