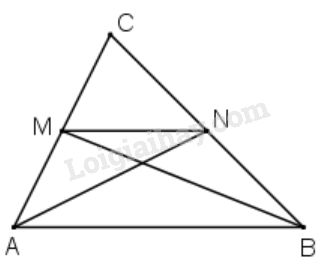
Bài 46 trang 133 SGK Toán 8 tập 1

Đề bài

Cho tam giác $ABC.$ Gọi $M, N$ là các trung điểm tương ứng của $AC, BC.$ Chứng minh rằng diện tích của hình thang $ABNM$ bằng $\dfrac{3}{4}$ diện tích của tam giác $ABC.$

Lời giải chi tiết

Vẽ hai trung tuyến $AN, BM$ của $∆ABC.$ Ta có:

 ${S_{MNA}} =\dfrac{1}{2}{S_{ACN}}$

(có cùng đường cao từ đỉnh $N$, đáy  $AM = \dfrac{1}{2}AC)$

 ${S_{ACN}} =\dfrac{1}{2}{S_{ABC}}$

(có cùng đường cao từ đỉnh $A$, đáy  $CN = \dfrac{1}{2}BC)$

 ${S_{ABN}} =\dfrac{1}{2}{S_{ABC}}$

(có cùng đường cao từ đỉnh $A$, đáy  $BN = \dfrac{1}{2}BC)$

Suy ra  ${S_{AMN}}= \dfrac{1}{2}{S_{ACN}} =\dfrac{1}{2}.\dfrac{1}{2}{S_{ABC}}$$=\dfrac{1}{4}{S_{ABC}}$

Vậy  ${S_{ABN}} + {S_{AMN}} = \dfrac{1}{2}{S_{ABC}} +\dfrac{1}{4}{S_{ABC}}$$=\dfrac{3}{4}S_{ABC}$

Tức là  ${S_{ABNM}} = \dfrac{3}{4}{S_{ABC}}$

HocTot.Nam.Name.Vn