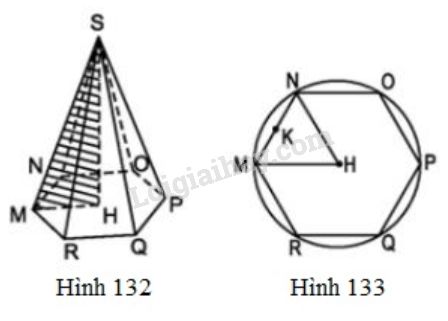
Bài 46 trang 124 SGK Toán 8 tập 2

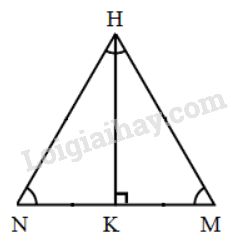
LG a.

 Diện tích đáy và thể tích của hình chóp (biết \(\sqrt{108}\approx 10,39\));

Phương pháp giải:

Tính thể tích hình chóp theo công thức:   \(V = \dfrac{1}{3} .S.h\), trong đó \(S\) là diện tích đáy, \(h\) là chiều cao.

Lời giải chi tiết:

Tam giác \(HMN \) là tam giác đều.

Đường cao của tam giác là:

 \(HK = \sqrt{HM^{2}- KM^{2}}\) \( = \sqrt{HM^{2}- {\left( {\dfrac{{MN}}{2}} \right)^2}} \)

\(= \sqrt{12^{2}- 6^{2}} = \sqrt{108}\approx  10,39(cm) \)

Diện tích đáy của hình chóp lục giác đều chính là \(6\) lần diện tích của tam giác đều \(HMN\).

Diện tích đáy của hình chóp là:  

   \(S_{đ} =6.\dfrac{1}{2}. MN. HK = 6.\dfrac{1}{2}. 12. 10,39 \) \(=374,04(cm^2) \) 

Thể tích của hình chóp:

  \(V =\dfrac{1}{3}. S_{đ}. SH = \dfrac{1}{3}. 374,04 . 35 \) \(= 4363,8(cm^3) \) 

LG b.

Độ dài cạnh bên \(SM\) và diện tích toàn phần của hình chóp (biết \(\sqrt{1333}\approx 36,51\) ).

Phương pháp giải:

Sử dụng định lý Pytago 

Diện tích xung quanh bằng nửa chu vi đáy nhân với trung đoạn 

Diện tích toàn phần bằng tổng diện tích xung quanh và diện tích đáy

Lời giải chi tiết:

Trong tam giác vuông \(SMH\) có: 

\(SM= \sqrt{SH^{2}+ MH^{2}} = \sqrt{35^{2}+ 12^{2}}\) \(=\sqrt{1369} = 37 (cm)\) 

Đường cao của mỗi mặt bên là:

 \(d = SK =\sqrt{SM^{2}- KM^{2}} \)

= \(\sqrt{37^{2}- 6^{2}} = \sqrt{1333}\approx 36,51 (cm) \)

Diện tích xung quanh hình chóp là :

   \( S_{xq} =  p.d = \dfrac{1}{2}.6. MN. SK \)

                     \( =\dfrac{1}{2}. 6.12.36,51 = 1314,36 (cm^2)\)

Diện tích toàn phần của hình chóp là:

   \(S_{tp} = S_{xq} +S_{đ} = 1314,36 + 374,04 \) \(= 1688,4 (cm^2) \)

HocTot.Nam.Name.Vn