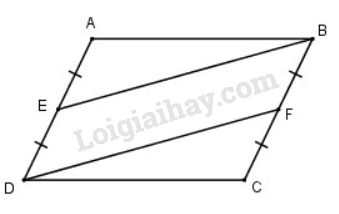
Bài 44 trang 92 SGK Toán 8 tập 1Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh rằng BE = DF. Đề bài Cho hình bình hành \(ABCD\). Gọi \(E\) là trung điểm của \(AD\), \(F\) là trung điểm của \(BC\). Chứng minh rằng \(BE = DF\). Video hướng dẫn giải Phương pháp giải - Xem chi tiết Áp dụng: +) Hình bình hành có các cặp cạnh đối song song và bằng nhau. +) Dấu hiệu nhận biết hình bình hành: Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành. Lời giải chi tiết
\(ABCD\) hình bình hành nên \(DE // BF\) và \(AD=BC\) \(E\) là trung điểm của \(AD\) (giả thiết) nên \(DE = \dfrac{1}{2}AD\) (tính chất trung điểm) \(F\) là trung điểm của \(BC\) (giả thiết) nên \(BF= \dfrac{1}{2}BC\) (tính chất trung điểm) Mà \(AD=BC\) (chứng minh trên) nên \(DE=BF\) Tứ giác \(BEDF\) có \(DE//BF\) và \(DE=BF\) (chứng minh trên) \( \Rightarrow \) Tứ giác \(BEDF\) là hình bình hành (theo dấu hiệu nhận biết hình bình hành). \( \Rightarrow \) \(BE = DF\) (tính chất hình bình hành). Cách khác: + \(ABCD\) là hình bình hành \(⇒ AB = CD, AD = BC, \widehat A=\widehat C.\) + \(E\) là trung điểm của \(AD\) \( ⇒ AE = \dfrac{1}{2}AD\) (tính chất trung điểm) \(F\) là trung điểm của \(BC \) \(⇒ BF= \dfrac{1}{2}BC\) (tính chất trung điểm) Mà \(AD = BC\) (chứng minh trên) \(⇒ AE = CF\) + Xét \(ΔAEB\) và \(ΔCFD\) có: \(AB = CD, \widehat A=\widehat C, AE = CF\) (chứng minh trên) \(⇒ ΔAEB = ΔCFD (c.g.c)\) \(⇒ EB = DF.\) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
