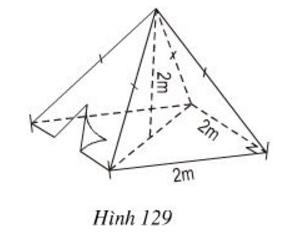
Bài 44 trang 123 SGK Toán 8 tập 2

LG a.

Thể tích không khí bên trong lều là bao nhiêu?

Phương pháp giải:

- Thể tích không khí trong lều bằng thể tích hình chóp có chiều cao \(2cm\), đáy là hình vuông cạnh dài \(2m\). 

Tính thể tích hình chóp theo công thức:   \(V = \dfrac{1}{3} .S.h\), trong đó \(S\) là diện tích đáy, \(h\) là chiều cao.

Lời giải chi tiết:

Thể tích cần tính bằng thể tích của hình chóp có chiều cao \(2cm\), đáy là hình vuông cạnh dài \(2m\). 

Diện tích đáy là:

           \( S_{đ} = 2.2=4(m^2)\)

Thể tích hình chóp là:

           \(V = \dfrac{1}{3}.S.h = \dfrac{1}{3}.4.2 = \dfrac{8}{3}\approx 2,67\)\(\,(m^3) \)  

LG b.

Xác định số vải bạt cần thiết để dựng lều (không tính đến đường viền, nếp gấp…biết \( \sqrt{5}\approx 2,24 \).

Phương pháp giải:

- Số vải bạt cần tính chính là diện tích của bốn mặt (hay là diện tích xung quanh), mỗi mặt là một tam giác cân.

Lời giải chi tiết:

Số vải bạt cần tính chính là diện tích của bốn mặt (hay là diện tích xung quanh) mỗi mặt là một tam giác cân.

Gọi \(H\) là trung điểm của \(AB\) và \(O\) là tâm của hình vuông \(ABCD\).

Để tính diện tích xung quanh ta cần phải tính được trung đoạn tức là đường cao \(SH\) của mỗi mặt.

 Theo định lý Pytago trong tam giác vuông SHA, ta có:

 \(SH^2 =SO^2+OH^2 \)\(\,= SO^2+{\left( {\dfrac{{BC}}{2}} \right)^2} \) \(= 2^2+1^2=5\)

\( \Rightarrow SH =\sqrt{5}\approx 2,24(m) \)

Diện tích xung quanh của hình chóp là: 

\( S_{xq} = p.d = \dfrac{1}{2}. 2.4.2,24 = 8,96 (m^2) \)

HocTot.Nam.Name.Vn