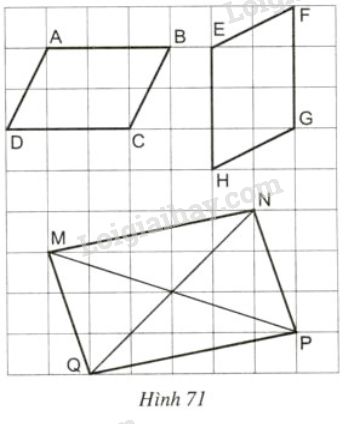
Bài 43 trang 92 SGK Toán 8 tập 1Các tứ giác ABCD, EFGH, MNPQ trên giấy kẻ ô vuông ở hình 71 có là hình bình hành hay không ? Đề bài Các tứ giác \(ABCD, EFGH, MNPQ\) trên giấy kẻ ô vuông ở hình \(71\) có là hình bình hành hay không ?
Video hướng dẫn giải Phương pháp giải - Xem chi tiết Áp dụng dấu hiệu nhận biết hình bình hành: +) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành. +) Tứ giác có các cạnh đối bằng nhau là hình bình hành. Lời giải chi tiết Cả ba tứ giác đều là hình bình hành. - Tứ giác \(ABCD\) là hình bình hành vì có: \(AB // CD\) và \(AB = CD =3\) (Tứ giác có 2 cạnh đối song song và bằng nhau ) - Tứ giác \(EFGH\) là hình bình hành vì có: \(EH // FG\) và \(EH = FG = 3\) (Tứ giác có 2 cạnh đối song song và bằng nhau ) - Tứ giác \(MNPQ\) có: \(MN\) và \(PQ\) là cạnh huyền của tam giác vuông có hai cạnh góc vuông là \(1\) và \(5\). Áp dụng định lí Py-ta-go ta có: \(MN = PQ = \sqrt {{5^2} + {1^2}} = \sqrt {26} \) \(MQ\) và \(NP\) là cạnh huyền của tam giác vuông có hai cạnh góc vuông là \(1\) và \(3\) Áp dụng định lí Py-ta-go ta có: \(MQ = NP = \sqrt {{3^2} + {1^2}} = \sqrt {10} \) Do đó \(MNPQ\) là hình bình hành vì có \(MN = PQ\) và \(MQ = NP\) (Tứ giác có các cạnh đối bằng nhau). HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
