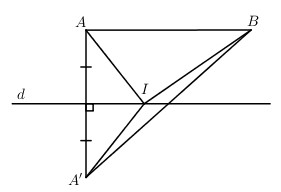
Bài 4 trang 99 SGK Hình học 12

LG a

Chứng minh rằng hai đường thẳng $d$ và $AB$ cùng nằm trong một mặt phẳng.

Phương pháp giải:

Chứng minh AB // d. Suy ra AB và d cùng thuộc một mặt phẳng.

Lời giải chi tiết:

Đường thẳng $AB$ có vectơ chỉ phương $\overrightarrow {AB} =(6; -4; 4)$

Đường thẳng $(d)$ có vectơ chỉ phương $\overrightarrow a  = (3; -2; 2)$

$\Rightarrow$ $\overrightarrow {AB}  = 2\overrightarrow a$  và  $A ∉ (d)$

$\Rightarrow  AB$ và $(d)$ song song với nhau.

$\Rightarrow$ Hai đường thẳng $(d)$ và $AB$ cùng thuộc một mặt phẳng.

LG b

Tìm điểm $I$ trên $d$ sao cho $AI + BI$ nhỏ nhất.

Phương pháp giải:

Gọi A' là điểm đối xứng với A qua d, khi đó ta có IA = IA' $\Rightarrow IA + IB = IA' + IB \ge A'B$.

Dấu bằng xảy ra $\Leftrightarrow I = d \cap A'B$.

Lời giải chi tiết:

Gọi $A'$ là điểm đối xứng của điểm $A$ qua phép đối xứng qua đường thẳng $d$ thì điểm $I$ cần tìm là giao điểm của đường thẳng $A'B$ và đường thẳng $d$.

Trong câu a) ta chứng minh được $AB // d$, từ đó suy ra $I$ chính là giao điểm của đường thẳng $d$ với mặt phẳng trung trực của đoạn thẳng $AB$.

Gọi $M$ là trung điểm của $AB$ thì $M(4; 0; 1)$.

Phương trình mặt phẳng trung trực của $AB$:

$3(x - 4) - 2(y - 0) + 2(z - 1) = 0$ $\Rightarrow  3x - 2y + 2z - 14 = 0$

Phương trình tham số của $(d)$:$\left\{ \matrix{ x = - 1 + 3t \hfill \cr  y = 2 - 2t \hfill \cr  z = 2 + 2t \hfill \cr} \right.$

Giá trị tham số ứng với giao điểm $I$của $(d)$ và mặt phẳng trung trực của $AB$ là nghiệm của phương trình:

$3( -1 + 3t) - 2(2 - 2t) + 2(2 + 2t) - 14 = 0$ $\Rightarrow  t = 1$

Từ đây ta được $I (2; 0; 4)$

Cách khác:

Gọi M là trung điểm của AB, H là giao điểm của AA’ với d.

IH//AB, H là trung điểm AA’ nên I là trung điểm A’B.

Mà M là trung điểm AB nên MI là đường trung bình của tam giác AA’B.

$\Rightarrow MI//AA'$, mà $AA' \bot d \Rightarrow MI \bot d$.

Ta có: $M\left( {4;0;1} \right)$, $I\left( { - 1 + 3t;2 - 2t;2 + 2t} \right)$

$\Rightarrow \overrightarrow {MI}  = \left( { - 5 + 3t;2 - 2t;1 + 2t} \right)$

$\overrightarrow {{u_d}}  = \left( {3; - 2;2} \right)$

$MI \bot d \Rightarrow \overrightarrow {MI} .\overrightarrow {{u_d}}  = 0$ $\Leftrightarrow 3\left( { - 5 + 3t} \right) - 2\left( {2 - 2t} \right) + 2\left( {1 + 2t} \right) = 0$

$\Leftrightarrow  - 15 + 9t - 4 + 4t + 2 + 4t = 0$

$\begin{array}{l} \Leftrightarrow  - 17 + 17t = 0\\ \Leftrightarrow t = 1\\ \Rightarrow I\left( {2;0;4} \right)\end{array}$

HocTot.Nam.Name.Vn