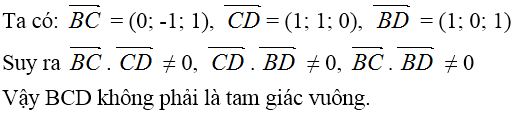Bài 4 trang 94 SGK Hình học 12

Đề bài

Trong không gian \(Oxyz\) cho bốn điểm \(A(1; 0; 0), B(0; 1; 0), C(0; 0; 1)\) và \(D(1; 1; 1)\)

Trong các mệnh đề sau, mệnh đề nào sai?

(A) Bốn điểm A, B, C, D tạo thành một tứ diện ;

(B) Tam giác ABD là tam giác đều ;

(C) \(AB ⊥ CD\) ;

(D) Tam giác \(BCD\) là tam giác vuông.

Lời giải chi tiết

Ta có: phương trình đoạn chắn mặt phẳng (ABC) là: \(\dfrac{x}{1} + \dfrac{y}{1} + \dfrac{z}{1} = 1 \) \(\Leftrightarrow x + y + z - 1 = 0\).

Dễ thấy điểm D không thuộc (ABC) nên bốn điểm A, B, C, D không đồng phẳng.

Mệnh đề A đúng.

Ta có: 

\(\begin{array}{l}
AB = \sqrt {{{\left( {0 - 1} \right)}^2} + {{\left( {1 - 0} \right)}^2} + {{\left( {0 - 0} \right)}^2}} = \sqrt 2 \\
AD = \sqrt {{{\left( {1 - 1} \right)}^2} + {{\left( {1 - 0} \right)}^2} + {{\left( {1 - 0} \right)}^2}} = \sqrt 2 \\
BD = \sqrt {{{\left( {1 - 0} \right)}^2} + {{\left( {1 - 1} \right)}^2} + {{\left( {1 - 0} \right)}^2}} = \sqrt 2 \\
\Rightarrow AB = AD = BD
\end{array}\)

Do đó tam giác ABD đều, mệnh đề B đúng.

\(\eqalign{
& \overrightarrow {AB} = ( - 1;1;0) \cr
& \overrightarrow {CD} = (1;1;0) \cr
& \overrightarrow {AB} .\overrightarrow {CD} = - 1.1 + 1.1 + 0.0 = 0 \cr} \)

Mệnh đề C đúng.

 

Chọn (D)

HocTot.Nam.Name.Vn