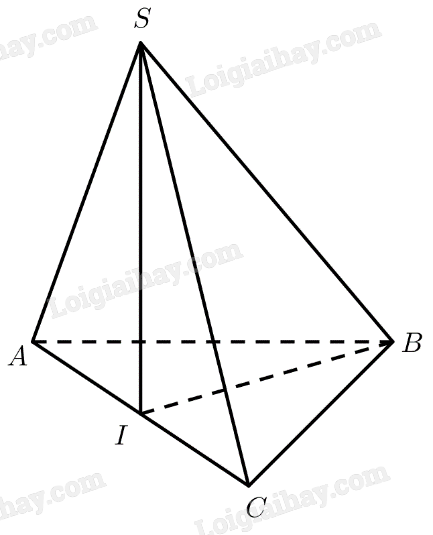
Bài 4 trang 64 SGK Toán 11 tập 2 – Chân trời sáng tạo

Đề bài

Cho hình chóp $S.ABC$ có $SA = SB = SC = a,\widehat {ASB} = 90^\circ ,\widehat {BSC} = {60^ \circ }$ và $\widehat {ASC} = {120^ \circ }$. Gọi $I$ là trung điểm cạnh $AC$. Chứng minh $SI \bot \left( {ABC} \right)$.

Lời giải chi tiết

 

Xét tam giác $SAC$ có:

$AC = \sqrt {S{A^2} + S{C^2} - 2.SA.SC.\cos \widehat {ASC}}  = a\sqrt 3$

$SI$ là trung tuyến $\Rightarrow SI = \frac{{\sqrt {2\left( {S{A^2} + S{C^2}} \right) - A{C^2}} }}{2} = \frac{a}{2}$

Ta có: $S{I^2} + A{I^2} = {\left( {\frac{a}{2}} \right)^2} + {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = {a^2} = S{A^2}$

$\Rightarrow \Delta SAI$ vuông tại $I \Rightarrow SI \bot AC$

Xét tam giác $SAB$ vuông tại $S$ có: $AB = \sqrt {S{A^2} + S{B^2}}  = a\sqrt 2$

Xét tam giác $SBC$ cân tại $S$ có $\widehat {BSC} = {60^ \circ }$ nên tam giác $SBC$ đều. Vậy  $BC = a$

Xét tam giác $ABC$ có: $A{B^2} + B{C^2} = {\left( {a\sqrt 2 } \right)^2} + {a^2} = 3{a^2} = A{C^2}$

$\Rightarrow \Delta ABC$ vuông tại $B \Rightarrow BI = \frac{1}{2}AC = \frac{{a\sqrt 3 }}{2}$

Xét tam giác $SBI$ có: $S{I^2} + B{I^2} = {\left( {\frac{a}{2}} \right)^2} + {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = {a^2} = S{B^2}$

$\Rightarrow \Delta SBI$ vuông tại $I \Rightarrow SI \bot BI$

Ta có:

$\left. \begin{array}{l}SI \bot AC\\SI \bot BI\end{array} \right\} \Rightarrow SI \bot \left( {ABC} \right)$