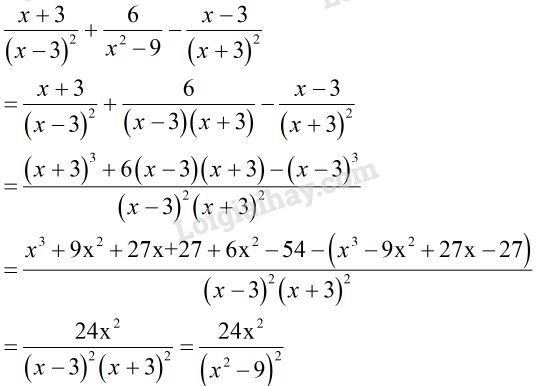Bài 4 trang 130 SGK Toán 8 tập 2Rút gọn rồi tính giá trị của biểu thức sau tại Đề bài Rút gọn rồi tính giá trị của biểu thức sau tại x=−13x=−13: [x+3(x−3)2+6x2−9−x−3(x+3)2][x+3(x−3)2+6x2−9−x−3(x+3)2].[1:(24x2x4−81−12x2+9)].[1:(24x2x4−81−12x2+9)] Video hướng dẫn giải Phương pháp giải - Xem chi tiết - Qui đồng cùng mẫu thức rồi rút gọn biểu thức. - Thay giá trị tương ứng của xx vào biểu thức sau khi đã rút gọn để tính giá trị của biểu thức đó. Lời giải chi tiết Điều kiện: x≠±3x≠±3 + Ngoặc vuông thứ nhất:
+ Ngoặc vuông thứ hai: 1:(24x2x4−81−12x2+9)=1:[24x2(x2−9)(x2+9)−12x2+9]=1:(24x2−12(x2−9)(x2−9)(x2+9))=1:12x2+108(x2−9)(x2+9)=1.(x2−9)(x2+9)12x2+108=(x2−9)(x2+9)12x2+108=(x2−9)(x2+9)12(x2+9)=x2−912 Nên [x+3(x−3)2+6x2−9−x−3(x+3)2].[1:(24x2x4−81−12x2+9)] =24x2(x2−9)2.x2−912=2x2x2−9 Tại x=−13 giá trị của biểu thức là: 2(−13)2(−13)2−9=2.1919−9=29−809=−140 HocTot.Nam.Name.Vn
|