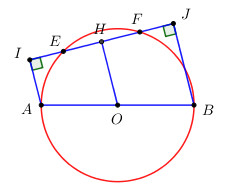
Bài 4 trang 128 Tài liệu dạy – học Toán 9 tập 1

Đề bài

Cho đường tròn đường kính AB và dây EF không cắt đường kính. Gọi I và J lần lượt là chân các đường vuông góc kẻ từ A và B đến EF. Chứng minh IE = JF.

Lời giải chi tiết

 

Ta có $\left\{ \begin{array}{l}AI \bot EF\\BJ \bot EF\end{array} \right. \Rightarrow AI//BJ \Rightarrow AIJB$ là hình thang.

Kẻ $OH//AI//BJ$, gọi $O$ là trung điểm của AB, áp dụng tính chất đường trung bình của hình thang ta suy ra H là trung điểm của IJ $\Rightarrow HI = HJ$ (1).

Ta có $\left\{ \begin{array}{l}OH//AI\\AI \bot EF\end{array} \right. \Rightarrow OH \bot EF \Rightarrow H$ là trung điểm của $EF$ (quan hệ vuông góc giữa đường kính và dây cung) $\Rightarrow HE = HF$ (2).

Từ (1) và (2) $\Rightarrow HI - HE = HJ - HF$

$\Leftrightarrow IE = JF$.

 HocTot.Nam.Name.Vn