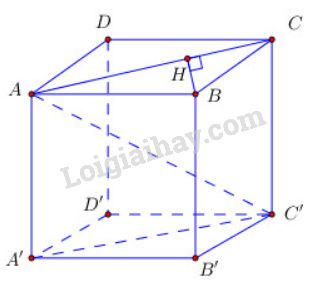
Bài 4 trang 119 SGK Hình học 11

Đề bài

Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có $AB =  a, BC= b, CC' = c$.

a) Tính khoảng cách từ $B$ đến mặt phẳng $(ACC'A')$.

b) Tính khoảng cách giữa hai đường thẳng $BB'$ và $AC'$.

Lời giải chi tiết

a) Trong $(ABCD)$ kẻ $BH \bot AC\,\,\left( {H \in AC} \right)\,\,\,\,\left( 1 \right)$

Ta có: $CC'\bot (ABCD)\Rightarrow CC'\bot BH\,\,\,\left( 2 \right)$

Từ (1) và (2) suy ra $BH\bot (ACC'A')$.

Áp dụng hệ thức lượng trong tam giác vuông $ABC$ ta có:

$\dfrac{1}{{B{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{B{C^2}}}$ $= \dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}} = \dfrac{{{a^2} + {b^2}}}{{{a^2}{b^2}}}$$\Rightarrow BH = \dfrac{{ab}}{{\sqrt {{a^2} + {b^2}} }}$

Cách khác:

Ta có:

$\begin{array}{l} \left\{ \begin{array}{l} AA' \bot \left( {ABCD} \right)\\ AA' \subset \left( {ACC'A'} \right) \end{array} \right.\\ \Rightarrow \left( {ACC'A'} \right) \bot \left( {ABCD} \right)\\ \left\{ \begin{array}{l} \left( {ACC'A'} \right) \cap \left( {ABCD} \right) = AC\\ BH \subset \left( {ABCD} \right)\\ BH \bot AC \end{array} \right.\\ \Rightarrow BH \bot \left( {ACC'A'} \right)\\ AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {b^2}} \\ BH.AC = AB.BC\\ \Rightarrow BH = \dfrac{{AB.BC}}{{AC}} = \dfrac{{ab}}{{\sqrt {{a^2} + {b^2}} }} \end{array}$

b) Ta có: $AC'\subset (ACC'A') // BB'$

$\Rightarrow d(BB', AC') =d(BB';(ACC'A')$$= d(B,(ACC'A'))=BH.$

$\Rightarrow d\left( {BB';AC'} \right) = \dfrac{{ab}}{{\sqrt {{a^2} + {b^2}} }}$

HocTot.Nam.Name.Vn