Bài 4 trang 40 SGK Hình học 10

Đề bài

Chứng minh rằng với mọi góc $α \, (0^0≤ α ≤ 180^0)$ ta đều có $\sin ^2\alpha  + {\cos ^2}\alpha  = 1.$

Lời giải chi tiết

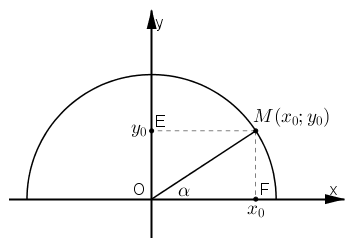
Vẽ nửa đường tròn đơn vị tâm O, bán kính 1 : (O; 1).

Lấy góc α bất kì (0º ≤ α ≤ 180º), luôn  tồn tại điểm M(x₀; y₀) thuộc nửa đường tròn sao cho $\widehat {xOM} = \alpha$

Khi đó ta có: $\sin \alpha  = \frac{{MF}}{{OM}}= MF$ $\cos \alpha  = \frac{{OF}}{{OM}} = OF$; .

($OM = 1$ do $M \in O\;(0,1)$).

Ta có:

${{{\sin }^2}\alpha  + {{\cos }^2}\alpha  = M{F^2} + O{F^2} = O{M^2} = {1^2} = 1}$

${ \Rightarrow {{\sin }^2}\alpha  + {{\cos }^2}\alpha  = 1}$

 

HocTot.Nam.Name.Vn