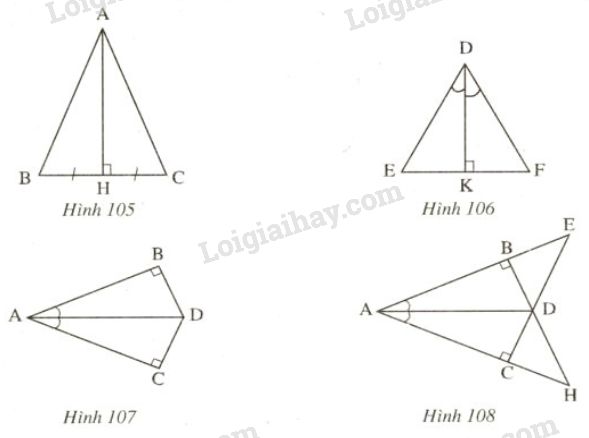
Bài 39 trang 124 SGK Toán 7 tập 1Trên mỗi hình 105, 106, 107, 108 các tam giác vuông nào bằng nhau? Vì sao? Đề bài Trên mỗi hình 105, 106, 107, 108 các tam giác vuông nào bằng nhau? Vì sao?
Video hướng dẫn giải Phương pháp giải - Xem chi tiết - Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau. - Nếu hai cạnh và một góc xen giữa của tam giác này bằng hai cạnh và một góc xen giữa của tam giác vuông kia thì hai tam giác đó bằng nhau. - Hệ quả: Nếu cạnh huyền và góc nhọn của tam giác vuông nay bằng cạnh huyền, góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. Lời giải chi tiết Hình 105 Xét ∆ABHΔABH và ∆ACHΔACH có: +) BH=CHBH=CH (giả thiết) +) ^AHB=^AHC=90oˆAHB=ˆAHC=90o +) AHAH cạnh chung ⇒∆ABH=∆ACH⇒ΔABH=ΔACH (c.g.c) Hình 106 Xét ∆DKEΔDKE và ∆DKFΔDKF có: +) ^EDK=^FDKˆEDK=ˆFDK (giả thiết) +) DKDK cạnh chung +) ^DKE=^DKF=90oˆDKE=ˆDKF=90o ⇒∆DKE=∆DKF⇒ΔDKE=ΔDKF (g.c.g) Hình 107 Áp dụng định lí tổng ba góc của một tam giác vào ∆ABDΔABD và ∆ACDΔACD ta có: ^ABD+^BDA+^DAB=1800(1)^ACD+^CDA+^DAC=1800(2) Mặt khác ta có: ^DAB=^DAC(giảthiết)(3)^ABD=^ACD=900(4) Từ (1), (2), (3), (4) suy ra ^BDA=^CDA Xét ∆ABD và ∆ACD có: +) ^DAB=^DAC(giảthiết) +) AD cạnh chung +) ^BDA=^CDA (chứng minh trên) ⇒∆ABD=∆ACD (g.c.g) Cách khác: Xét ∆ABD vuông tại B và ∆ACD vuông tại C, ta có: +) ^DAB=^DAC(giảthiết) +) AD cạnh chung ⇒∆ABD=∆ACD (cạnh huyền-góc nhọn) Hình 108 Áp dụng định lí tổng ba góc của một tam giác vào ∆ABD và ∆ACD ta có: ^ABD+^BDA+^DAB=1800(5)^ACD+^CDA+^DAC=1800(6) Mặt khác ta có: ^DAB=^DAC(giảthiết)(7)^ABD=^ACD=900(8) Từ (5), (6), (7), (8) suy ra ^BDA=^CDA Xét ∆ABD và ∆ACD có: +) ^DAB=^DAC(giảthiết) +) AD cạnh chung +) ^BDA=^CDA (chứng minh trên) ⇒∆ABD=∆ACD (g.c.g) ⇒BD=CD (hai cạnh tương ứng ) ⇒AB=AC (hai cạnh tương ứng ) (Hoặc ta có thể chứng minh ∆ABD=∆ACD theo trường hợp cạnh huyền - góc nhọn) Xét ∆DBE và ∆DCH +) ^EBD=^HCD=900 +) BD=CD (chứng minh trên) +) ^BDE=^CDH (đối đỉnh) ⇒∆DBE=∆DCH (g.c.g) ⇒DE=DH (hai cạnh tương ứng) Xét ∆ABH và ∆ACE +) ˆA chung +) AB=AC (chứng minh trên) +) ^ABH=^ACE=900 ⇒∆ABH=∆ACE (g.c.g) ⇒AH=AE (hai cạnh tương ứng) Xét ∆ADE và ∆ADH +) Cạnh AD chung +) AE=AH (chứng minh trên) +) DE=DH (chứng minh trên) ⇒∆ADE=∆ADH (c.c.c) HocTot.Nam.Name.Vn
|