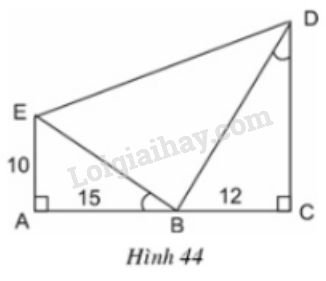
Bài 37 trang 79 SGK Toán 8 tập 2

LG a.

Trong hình vẽ, có bao nhiêu tam giác vuông? Hãy kể tên các tam giác đó.

Phương pháp giải:

Áp dụng: Tam giác có 1 góc vuông là tam giác vuông.

Lời giải chi tiết:

Ta có: $\widehat{EBA} = \widehat{BDC}$ (giả thiết) mà $\widehat{BDC} + \widehat{CBD}={90^0}$ (do tam giác BCD vuông tại C) 

$\Rightarrow \widehat{EBA} + \widehat{CBD}={90^0}$ 

Vậy $\widehat{EBD} = {180^0} - (\widehat{EBA}+ \widehat{CBD})$$\, = {180^o} - {90^o} = {90^o}$

Vậy trong hình vẽ có ba tam giác vuông đó là:

$∆ABE, ∆CBD, ∆EBD.$ 

LG b.

Cho biết $AE = 10cm, AB = 15cm, BC = 12cm$. Hãy tính độ dài các đoạn thẳng $CD, BE, BD$ và $ED$ (làm tròn đến chữ số thập phân thứ nhất).

Phương pháp giải:

Áp dụng:

- Định lí: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.

- Tính chất hai tam giác đồng dạng.

- Định lí Pitago.

Lời giải chi tiết:

$∆ABE$ và $∆CDB$ có:

$\widehat{A} = \widehat{C}=90^o$

$\widehat{ABE}= \widehat{CDB}$ (giả thiết)

$\Rightarrow  ∆ABE ∽ ∆CDB$ (g-g)

$\Rightarrow \dfrac{AB}{CD} = \dfrac{AE}{CB}$ (tính chất hai tam giác đồng dạng)

$\Rightarrow CD = \dfrac{AB.CB}{AE} = 18\, (cm)$

- Áp dụng định lí pitago ta có:

$∆ABE$ vuông tại $A$

$\Rightarrow  BE = \sqrt{AE^{2}+AB^{2}}$ $\,=\sqrt{10^{2}+15^{2}}$ $\approx  18\, (cm)$.

 $∆BCD$ vuông tại $C$

$\Rightarrow BD = \sqrt {B{C^2} + D{C^2}}$ $= \sqrt {{{12}^2} + {{18}^2}}  \approx 21,6\,\,cm$

$∆EBD$ vuông tại $B$

$\Rightarrow  ED = \sqrt{EB^{2}+BD^{2}}$ $=\sqrt{325+ 468} \approx 28,2\, (cm)$

LG c.

So sánh diện tích tam giác $BDE$ với tổng diện tích hai tam giác $AEB$ và $BCD$.

Phương pháp giải:

Sử dụng: Công thức tính diện tích tam giác, diện tích hình thang.

Lời giải chi tiết:

Ta có: 

$S_{ABE} + S_{DBC}$

$= \dfrac{1}{2}AE.AB + \dfrac{1}{2}BC.CD$ 

$= \dfrac{1}{2}. 10.15 + \dfrac{1}{2}.12.18$

$= 75 + 108 = 183\;cm^2$.

Ta có: $A{\rm{E}}//DC\,\,\left(\text{ cùng } { \bot AC} \right) \Rightarrow$ $ACDE$ là hình thang.

$S_{ACDE} = \dfrac{1}{2}.(AE + CD).AC$

$= \dfrac{1}{2}.(10 + 18).27= 378\;cm^2$

$\Rightarrow S_{EBD} = S_{ACDE} - (S_{ABE}+ S_{DBC})$$\; = 378 - 183 = 195\,cm^2$

$S_{EBD}> S_{ABE} + S_{DBC}$ $( 195 > 183)$.

Cách khác: 

Các em có thể thay độ dài BE, BD tính được ở câu b để tính diện tích tam giác EBD.

HocTot.Nam.Name.Vn