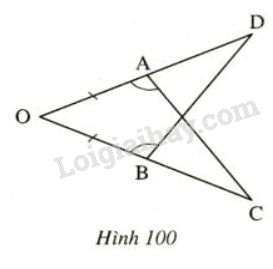
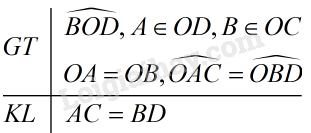Bài 36 trang 123 SGK Toán 7 tập 1Trên hình 100 ta có OA=OB, OAC=OBD. Đề bài Trên hình 100 ta có \(OA=OB\), \(\widehat{OAC}=\widehat{OBD}\). Chứng minh rằng \(AC=BD.\)
Video hướng dẫn giải Phương pháp giải - Xem chi tiết Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và góc kề của tam giác kia thì hai tam giác đó bằng nhau. Lời giải chi tiết
Xét \(∆OAC\) và \(∆OBD\) có: + \(\widehat{OAC} = \widehat{OBD}\) (giả thiết) + \(OA = OB\) (giả thiết) + \(\widehat{O}\) chung \( \Rightarrow ∆OAC = ∆OBD\) (g.c.g) \(\Rightarrow AC = BD\) (\(2\) cạnh tương ứng). HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
