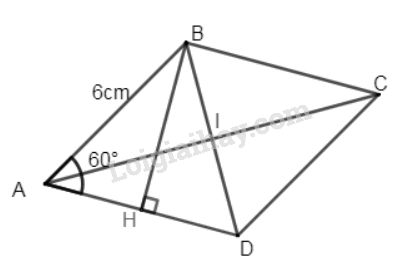
Bài 35 trang 129 SGK Toán 8 tập 1

Đề bài

Tính diện tích hình thoi có cạnh dài $6\,cm$ và một trong các góc của nó có số đo là $60^{\circ}$

Lời giải chi tiết

Xét hình thoi $ABCD$ có cạnh $6cm$ và $\widehat {BAD}=60^0$. Kẻ $BH\bot AD$

Công thức tổng quát tính độ dài đường cao BH: 

Ta có $∆ABD$ là tam giác đều (vì tam giác $ABD$ cân có  $\widehat{A}$ = $60^{\circ}$ )

Tam giác $ABD$ đều nên đường cao BH cũng là đường trung tuyến hay $H$ là trung điểm của $AD$

Suy ra $AH=\dfrac{AD}{2}=\dfrac{AB}{2}$

Áp dụng định lí Pytago vào tam giác vuông $ABH$ có:

$B{H^2} = A{B^2} - A{H^2}$

          $= A{B^2}-\left ( \dfrac{AB}{2} \right )^{2}$

          $= A{B^2}-\dfrac{AB^{2}}{4} = \dfrac{3AB^{2}}{4}$.

$\Rightarrow BH = \dfrac{AB.\sqrt{3}}2$ (cm)

Tổng quát: Đường cao tam giác đều cạnh $a$ có độ dài là: ${h_a}=\dfrac{a\sqrt{3}}2$

Áp dụng vào bài với cạnh $a=6cm$ thì $BH = \dfrac{a.\sqrt{3}}2 = \dfrac{6\sqrt{3}}2 = 3\sqrt3$ (cm)

Tính diện tích hình thoi ABCD.

Cách 1:

Ta có: $BH = 3\sqrt3$ (cm) (theo trên)

${S_{ABCD}}= BH. AD = 3\sqrt 3. 6$$\,= 18\sqrt 3\;(c{m^2})$

Cách 2:

Vì $∆ABD$ là tam giác đều nên $BD = AB = 6\,cm$, $AI$ là đường cao đồng thời là trung tuyến tam giác nên $AI = \dfrac{6\sqrt{3}}{2} = 3\sqrt3$ (cm)

$\Rightarrow AC =2AI= 6\sqrt 3$ (cm)

${S_{ABCD}}=\dfrac{1}{2} BD. AC = \dfrac{1}{2} 6. 6\sqrt 3$$\,= 18\sqrt 3\; (c{m^2})$

HocTot.Nam.Name.Vn