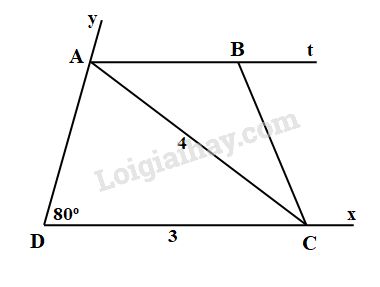
Bài 33 trang 83 SGK Toán 8 tập 1

Đề bài

Dựng hình thang cân \(ABCD\), biết đáy \(CD = 3\,cm\), đường chéo \(AC = 4\,cm\), \(\widehat D = {80^o}\).

Lời giải chi tiết

a) Phân tích

Giả sử dựng được hình thang \(ABCD\) theo yêu cầu đề bài.

Ta dựng được đoạn thẳng \(CD = 3\,cm.\)

Điểm \(A\) phải thỏa mãn hai điều kiện:

+) Tia \(DA\) tạo với \(DC\) một góc bằng \({80^o}\).

+) \(CA = 4\,cm\) nên \(A\) thuộc cung tròn tâm \(C\) bán kính \(4\,cm.\)

\(ABCD\) là hình thang nên \(AB // CD\)

Hình thang \(ABCD\) cân nên \(\widehat {BCD} = \widehat D = {80^o}\)

Vì vậy điểm \(B\) phải thỏa mãn \(2\) điều kiện:

+) \(B\) nằm trên đường thẳng đi qua \(A\) và song song với \(CD\).

+ Tia \(CB\) tạo với \(CD\) một góc \({80^o}\).

b) Cách dựng

- Dựng \(\widehat {xDy} = {80^o}\). Trên tia \(Dx\) dựng đoạn thẳng \(DC = 3cm\).

- Dựng cung tròn tâm \(C\) bán kính \(4\, cm\) cắt tia \(Dy\) tại \(A.\)

- Dựng tia \(At\) song song với  tia \(Dx\)

- Trên cùng một nửa mặt phẳng bờ \(DC\) chứa \(A\) dựng tia \(CB\) sao cho tia \(CB\) tạo với \(CD\) một góc \({80^o}\) và cắt tia \(At\) tại \(B\).

- Hình thang \(ABCD\) là hình thang cần dựng.

c) Chứng minh

Theo cách dựng ta có \(AB // CD\) và \(AC  = 4cm\); \(DC = 3cm\); \(\widehat {BCD} = \widehat D = {80^o}\)

Suy ra tứ giác \(ABCD\) là hình thang cân thỏa mãn điều kiện bài toán.

d) Biện luận

Ta luôn dựng được một hình thang thỏa mãn điều kiện đề bài.

HocTot.Nam.Name.Vn