Bài 33 trang 77 SGK Toán 8 tập 2

Đề bài

Chứng minh rằng nếu tam giác $A'B'C'$ đồng dạng với tam giác $ABC$ theo tỉ số $k$, thì tỉ số của hai đường trung tuyến tương ứng với hai tam giác đó cũng bằng $k$.

Lời giải chi tiết

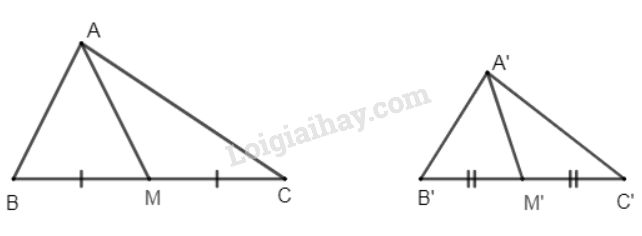
Giả sử $∆A'B'C'$ đồng dạng $∆ABC$ theo tỉ số $k, A'M', AM$ là hai đường trung tuyến tương ứng.

Vì $∆A'B'C'$ đồng dạng $∆ABC$ theo tỉ số k (giả thiết)

$\dfrac{A'B'}{AB} = \dfrac{B'C'}{BC} = k$ (tính chất hai tam giác đồng dạng)

Mà $B'C' = 2B'M', BC = 2BM$ (tính chất trung tuyến)

$\Rightarrow \dfrac{{A'B'}}{{AB}} = \dfrac{{2B'M'}}{{2BM}} = \dfrac{{B'M'}}{{BM}}$

Xét  $∆ABM$ và $∆A'B'M'$ có:

 $\widehat{B} = \widehat{B'}$ (vì $∆A'B'C'$ đồng dạng $∆ABC$) 

 $\dfrac{{A'B'}}{{AB}} = \dfrac{{B'M'}}{{BM}}$ (chứng minh trên)

$\Rightarrow ∆A'B'M'$ đồng dạng $∆ABM$ theo tỉ số $\frac{A'B'}{AB} = k$ (c-g-c)

$\Rightarrow \dfrac{A'M'}{AM}= \dfrac{A'B'}{AB} = k.$ (tính chất hai tam giác đồng dạng)