Bài 33 trang 128 SGK Toán 8 tập 1

Đề bài

Vẽ hình chữ nhật có một cạnh bằng đường chéo của một hình thoi cho trước và có diện tích bằng diện tích của hình thoi đó. Từ đó suy ra cách tính diện tích hình thoi.

Lời giải chi tiết

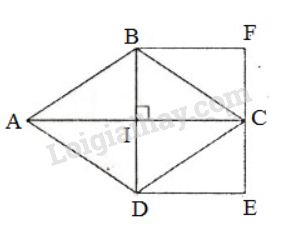
Cho hình thoi \(ABCD\) có hai đường chéo cắt nhau tại \(I\). Suy ra \(I\) là trung điểm \(AC\) hay \(IC=\dfrac{1}{2}\) \(AC\)  (tính chất)

Vẽ hình chữ nhật có một cạnh là đường chéo \(BD\), cạnh kia bằng \(IC\) ( \(IC=\dfrac{1}{2}\) \(AC\))

Khi đó diện tích của hình chữ nhật \(BFED\) bằng diện tích hình thoi \(ABCD\).

Thật vậy:

\({S_{BF{\rm{ED}}}} = BD.IC = B{\rm{D}}.\dfrac{1}{2}AC \)\(= \dfrac{1}{2}B{\rm{D}}.AC = {S_{ABC{\rm{D}}}}.\)

Từ đó suy ra cách tính diện tích hình thoi: Diện tích hình thoi bằng nửa tích hai đường chéo.

 HocTot.Nam.Name.Vn