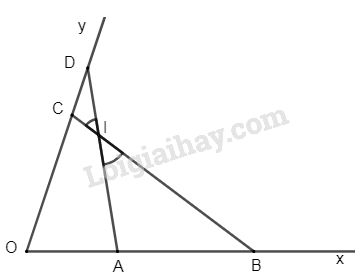
Bài 32 trang 77 SGK Toán 8 tập 2

Đề bài

Trên một cạnh của góc \(xOy\) (\(\widehat {xOy} \ne {180^0}\)), Đặt các đoạn thẳng \(OA= 5cm, OB= 16cm\). Trên cạnh thứ hai của góc đó, đặt các đoạn \(OC= 8cm, OD= 10cm\).

a) Chứng minh hai tam giác \(OCB\) và \(OAD\) đồng dạng.

b) Gọi giao điểm của các cạnh \(AD\) và \(BC\) là \(I\), chứng minh rằng hai tam giác \(IAB\) và \(ICD\) có các góc bằng nhau từng đôi một.

Lời giải chi tiết

a) Ta có:

\(\dfrac{OA}{OC} = \dfrac{5}{8}\) ; \(\dfrac{OD}{OB} = \dfrac{10}{16} = \dfrac{5}{8}\) 

 \(\Rightarrow \dfrac{OA}{OC} = \dfrac{OD}{OB}\)

Xét  \(∆OCB\) và \(∆OAD\) có:

+) \(\widehat O\) chung

+) \(\dfrac{OA}{OC} = \dfrac{OD}{OB}\) (chứng minh trên)

 \(\Rightarrow ∆OCB \) đồng dạng \(∆OAD\) ( c-g-c)

\( \Rightarrow \widehat {ODA} = \widehat {CBO}\) (2 góc tương ứng) hay \(\widehat{CDI}\) = \(\widehat{IBA}\) 

b) Xét \(∆ICD\) và \(∆IAB\) có

 \(\widehat{CID}\) = \(\widehat{AIB}\) (hai góc đối đỉnh)   (1)

\(\widehat{CDI}\) = \(\widehat{IBA}\) (theo câu a)            (2)

Theo định lí tổng ba góc trong một tam giác ta có:

\(\eqalign{
& \widehat {CID} + \widehat {CDI} + \widehat {ICD} = {180^0} \cr
& \widehat {AIB}+\widehat {IBA} + \widehat {IAB} = {180^0} \cr} \)

\( \Rightarrow \widehat {CID} + \widehat {CDI} + \widehat {ICD} \) \(= \widehat {AIB}+\widehat {IBA} + \widehat {IAB}\)   (3)

Từ (1), (2) và (3) suy ra: \( \widehat {ICD}=\widehat {IAB}\)

Vậy hai tam giác \(IAB\) và \(ICD\) có các góc bằng nhau từng đôi một. 

HocTot.Nam.Name.Vn