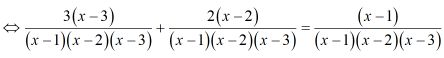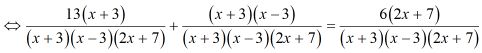Bài 31 trang 23 SGK Toán 8 tập 2

LG a.

\(\dfrac{1}{{x - 1}} - \dfrac{{3{x^2}}}{{{x^3} - 1}} = \dfrac{{2x}}{{{x^2} + x + 1}}\)

Phương pháp giải:

Bước 1: Tìm điều kiện xác định.

Bước 2: Qui đồng khử mẫu.

Bước 3: Giải phương trình bằng cách chuyển vế đưa về dạng phương trình tích.

*) Giải phương trình tích: \(A(x).B(x)=0\)

\( \Leftrightarrow A(x) = 0\) hoặc \(B(x) =0\)

Lời giải chi tiết:

\(\dfrac{1}{{x - 1}} - \dfrac{{3{x^2}}}{{{x^3} - 1}} = \dfrac{{2x}}{{{x^2} + x + 1}}\) (1)

Ta có: \(x - 1 ≠ 0 \Leftrightarrow x ≠ 1\) và \({x^3} - 1 \ne 0\) khi \(x^3 \ne 1\) hay \(x \ne 1\)

\(  {x^2+x + 1} = {{x^2} + x + \dfrac{1}{4} + \dfrac{3}{4}} \)

\( =  {{x^2} + 2.x.\dfrac{1}{2} + {{\left( {\dfrac{1}{2}} \right)}^2} + \dfrac{3}{4}}\)

\(= {{{\left( {x + \dfrac{1}{2}} \right)}^2} + \dfrac{3}{4}}\) 

Ta có: \({\left( {x + \dfrac{1}{2}} \right)^2} \geqslant 0\) với mọi \(x \in\mathbb R\) nên \({\left( {x + \dfrac{1}{2}} \right)^2} + \dfrac{3}{4} > 0\) với mọi \(x \in\mathbb R\)

Do đó: 

ĐKXĐ:  \(x ≠ 1\)

MTC= \({x^3} - 1=(x-1)(x^2+x+1)\)

Ta có:

(1) \(  \Leftrightarrow \dfrac{{{x^2} + x + 1}}{{{x^3} - 1}} - \dfrac{{3{x^2}}}{{{x^3} - 1}} = \dfrac{{2x\left( {x - 1} \right)}}{{{x^3} - 1}}\)

\(\Rightarrow {x^2} + x + 1 - 3{x^2} = 2x\left( {x - 1} \right) \)

\(\Leftrightarrow  - 2{x^2} + x + 1 = 2{x^2} - 2x\)

\( \Leftrightarrow 0 = 2{x^2} - 2x + 2{x^2} - x - 1\)

\( \Leftrightarrow 0 = 4{x^2} - 3x - 1\)

\(\Leftrightarrow 4{x^2} - 3x - 1 = 0\)

\(\Leftrightarrow 4{x^2} - 4x+x - 1 = 0\)

\(\Leftrightarrow 4x\left( {x - 1} \right) + \left( {x - 1} \right) = 0\)

\(\Leftrightarrow \left( {x - 1} \right)\left( {4x + 1} \right) = 0\)

\( \Leftrightarrow \left[ \begin{gathered}
x - 1 = 0 \hfill \\
4x + 1 = 0 \hfill \\ 
\end{gathered} \right.\)

\( \Leftrightarrow \left[ \begin{gathered}
x = 1 \hfill \\
4x = - 1 \hfill \\ 
\end{gathered} \right.\)

\(\Leftrightarrow \left[ {\matrix{{x = 1}\text{( loại)} \cr {x = - \dfrac{1}{4}}\text{(thỏa mãn)}\cr} }\right.\)

Vậy phương trình có nghiệm duy nhất \(x =  - \dfrac{1}{4}\)

LG b.

\(\dfrac{3}{{\left( {x - 1} \right)\left( {x - 2} \right)}} + \dfrac{2}{{\left( {x - 3} \right)\left( {x - 1} \right)}} \)\(\,= \dfrac{1}{{\left( {x - 2} \right)\left( {x - 3} \right)}}\)

Phương pháp giải:

Bước 1: Tìm điều kiện xác định.

Bước 2: Qui đồng khử mẫu.

Bước 3: Giải phương trình bằng cách chuyển vế đưa về dạng phương trình tích.

*) Giải phương trình tích: \(A(x).B(x)=0\)

\( \Leftrightarrow A(x) = 0\) hoặc \(B(x) =0\)

Lời giải chi tiết:

\(\dfrac{3}{{\left( {x - 1} \right)\left( {x - 2} \right)}} + \dfrac{2}{{\left( {x - 3} \right)\left( {x - 1} \right)}} \)\(\,= \dfrac{1}{{\left( {x - 2} \right)\left( {x - 3} \right)}}\) (2)

ĐKXĐ: \(x ≠ 1, x ≠ 2, x ≠ 3\)

MTC= \((x-1)(x-2)(x-3)\)

Ta có: (2) 

\( \Rightarrow 3\left( {x - 3} \right) + 2\left( {x - 2} \right) = x - 1\)

\(\Leftrightarrow 3x - 9 + 2x - 4 = x - 1\)

\( \Leftrightarrow 5x - 13 = x - 1\)

\( \Leftrightarrow 5x - x =  - 1 + 13\)

\(⇔ 4x = 12\)

\( \Leftrightarrow x = 12:4\)

\(⇔ x = 3\) (không thỏa mãn ĐKXĐ)

Vậy phương trình vô nghiệm.

LG c.

\(1 + \dfrac{1}{{x + 2}} = \dfrac{{12}}{{8 + {x^3}}}\)

Phương pháp giải:

Bước 1: Tìm điều kiện xác định.

Bước 2: Qui đồng khử mẫu.

Bước 3: Giải phương trình bằng cách chuyển vế đưa về dạng phương trình tích.

*) Giải phương trình tích: \(A(x).B(x)=0\)

\( \Leftrightarrow A(x) = 0\) hoặc \(B(x) =0\)

Lời giải chi tiết:

\(1 + \dfrac{1}{{x + 2}} = \dfrac{{12}}{{8 + {x^3}}}\)(3)

Ta có:  \(8 + {x^3} \ne 0\)\(\Leftrightarrow x^3  ≠ -8 ⇔ x ≠ -2\)

ĐKXĐ: \(x ≠ -2\)

MTC= \(8 + {x^3}=(x+2)(x^2-2x+4)\)

Ta có: (3) \( \Leftrightarrow \dfrac{{8 + {x^3}}}{{8 + {x^3}}} + \dfrac{{{x^2} - 2x + 4}}{{8 + {x^3}}} = \dfrac{{12}}{{8 + {x^3}}}\)

\( \Rightarrow {x^3} + 8 + {x^2} - 2x + 4 = 12 \)

\( \Leftrightarrow {x^3} + {x^2} - 2x = 12 - 8 - 4\)

\(\Leftrightarrow {x^3} + {x^2} - 2x = 0\)

\(\Leftrightarrow x\left( {{x^2} + x - 2} \right) = 0\)

\(\Leftrightarrow x\left[ {{x^2} + 2x - x - 2} \right] = 0\)

⇔\(x[ x(x+2) - (x+2) ] = 0\)

⇔ \(x(x + 2)(x - 1) = 0\)

\( \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x + 2 = 0\\
x - 1 = 0
\end{array} \right. \)

\(\Leftrightarrow \left[ \begin{array}{l}
x = 0\left( \text{ thỏa mãn} \right)\\
x = - 2\left( \text{ loại} \right)\\
x = 1\left( \text{ thỏa mãn} \right)
\end{array} \right.\)

Vậy phương trình có tập nghiệm là \(S = \left\{ {0;1} \right\}\).

LG d.

\(\dfrac{{13}}{{\left( {x - 3} \right)\left( {2x + 7} \right)}} + \dfrac{1}{{2x + 7}}\)\(\, = \dfrac{6}{{\left( {x - 3} \right)\left( {x + 3} \right)}}\)

Phương pháp giải:

Bước 1: Tìm điều kiện xác định.

Bước 2: Qui đồng khử mẫu.

Bước 3: Giải phương trình bằng cách chuyển vế đưa về dạng phương trình tích.

*) Giải phương trình tích: \(A(x).B(x)=0\)

\( \Leftrightarrow A(x) = 0\) hoặc \(B(x) =0\)

Lời giải chi tiết:

\(\dfrac{{13}}{{\left( {x - 3} \right)\left( {2x + 7} \right)}} + \dfrac{1}{{2x + 7}} \)\(\,= \dfrac{6}{{\left( {x - 3} \right)\left( {x + 3} \right)}}\) (4)

ĐKXĐ: \(x \ne 3,x \ne  - 3,x \ne  - \dfrac{7}{2}\)

MTC= \({\left( {x - 3} \right)\left( {x + 3} \right)}\left( {2x + 7} \right)\)

Ta có: (4)

\( \Rightarrow 13\left( {x + 3} \right) + \left( {x - 3} \right)\left( {x + 3} \right) \)\(= 6\left( {2x + 7} \right) \)

\(\Leftrightarrow 13x + 39 + {x^2} - 9 = 12x + 42\)

\(\Leftrightarrow {x^2} + 13x + 30 = 12x + 42\)

\( \Leftrightarrow {x^2} + 13x + 30 - 12x - 42 = 0\)

\(\Leftrightarrow {x^2} + x - 12 = 0\)

\(\Leftrightarrow {x^2} + 4x - 3x - 12 = 0\)

\(\Leftrightarrow x\left( {x + 4} \right) - 3\left( {x + 4} \right) = 0\)

\(\Leftrightarrow \left( {x - 3} \right)\left( {x + 4} \right) = 0\)

\( \Leftrightarrow \left[ \begin{array}{l}
x - 3 = 0\\
x + 4 = 0
\end{array} \right. \)

\(\Leftrightarrow \left[ \begin{array}{l}
x = 3\left( \text{không thỏa mãn} \right)\\
x = - 4\left( \text{thỏa mãn} \right)
\end{array} \right.\)

Vậy phương trình có tập nghiệm là \(S = \left\{-4 \right\}\). 

HocTot.Nam.Name.Vn