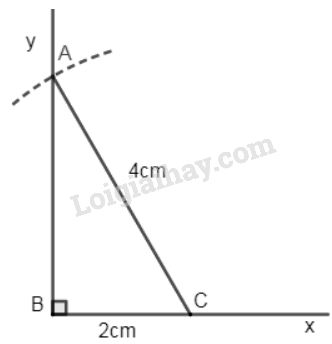
Bài 30 trang 83 SGK Toán 8 tập 1

Đề bài

Dựng tam giác \(ABC\) vuông tại \(B\), biết cạnh huyền \(AC = 4\,cm\), cạnh góc vuông \(BC = 2\,cm.\)

Lời giải chi tiết

a) Phân tích:

Giả sử dựng được \(ΔABC\) thỏa mãn yêu cầu.

Ta dựng được đoạn \(BC\) vì biết \(BC = 2cm.\)

Khi đó điểm \(A\) là giao điểm của:

+ Tia \(By\) vuông góc với \(BC\)

+ Cung tròn tâm \(C\) bán kính \(4\,cm.\)

b) Cách dựng:

- Dựng \(\widehat {xBy} = {90^0}\). Trên tia \(Bx\) lấy điểm \(C\) sao cho \(BC = 2\,cm.\)

- Dựng cung tròn \((C; 4\,cm)\) và cung tròn này cắt tia \(By\) tại \(A.\)

- Nối \(A\) với \(C\) ta được  \(∆ABC\) là tam giác cần dựng.

c) Chứng minh

\(ΔABC\) có \(\widehat B = {90^0}, BC = 2cm.\)

\(A\) thuộc cung tròn tâm \(C\) bán kính \(4\,cm\) nên \(AC = 4cm.\)

Vậy \(ΔABC\) thỏa mãn yêu cầu đề bài

d) Biện luận

Ta luôn dựng được một hình thang thỏa mãn điều kiện của đề bài.

HocTot.Nam.Name.Vn