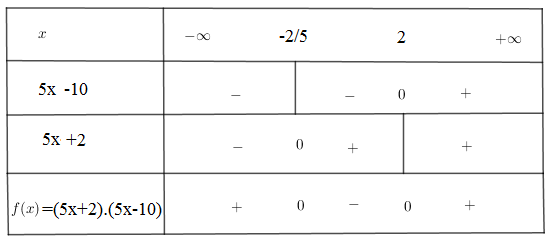
Bài 3 trang 94 SGK Đại số 10

LG a

\(|5x - 4| ≥ 6\);

Phương pháp giải:

\(\begin{array}{l}
\left| {f\left( x \right)} \right| \le a \Leftrightarrow  - a \le f\left( x \right) \le a\\
\left| {f\left( x \right)} \right| \ge a \Leftrightarrow \left[ \begin{array}{l}
f\left( x \right) \le  - a\\
f\left( x \right) \ge a
\end{array} \right.\\
\left( {a > 0} \right)
\end{array}\)

Lời giải chi tiết:

\(|5x - 4| ≥ 6\)

Cách 1:

\(\eqalign{
& \Leftrightarrow {(5x - 4)^2} \ge {6^2}\cr& \Leftrightarrow {(5x - 4)^2} - {6^2} \ge 0 \cr 
& \Leftrightarrow (5x - 4 - 6)(5x - 4 + 6) \ge 0 \cr 
& \Leftrightarrow (5x - 10)(5x + 2) \ge 0 \cr} \)

Bảng xét dấu:

Ta có:

\(\begin{array}{l}
5x - 10 = 0 \Leftrightarrow x = 2\\
5x + 2 = 0 \Leftrightarrow x =  - \dfrac{2}{5}
\end{array}\)

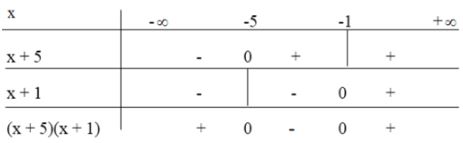
Từ bảng xét dấu cho tập nghiệm của bất phương trình: \(T =\left( { - \infty ; - {2 \over 5}} \right] ∪ [2; +∞)\).

Cách 2:

\(\begin{array}{l}
\left| {5x - 4} \right| \ge 6 \Leftrightarrow \left[ \begin{array}{l}
5x - 4 \ge 6\\
5x - 4 \le - 6
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
5x \ge 10\\
5x \le - 2
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x \ge 2\\
x \le - \dfrac{2}{5}
\end{array} \right.
\end{array}\)

Vậy tập nghiệm của bất phương trình: \(T =\left( { - \infty ; - {2 \over 5}} \right] ∪ [2; +∞)\).

LG b

\(\left | \dfrac{-5}{x+2} \right |<\left | \dfrac{10}{x-1} \right |.\)

Lời giải chi tiết:

\(\left | \dfrac{-5}{x+2} \right |<\left |\dfrac{10}{x-1} \right |\)

Cách 1:

\(\eqalign{
& \Leftrightarrow {5 \over {|x + 2|}} < {{10} \over {|x - 1|}} \cr &\left( {DK:x \ne - 2,x \ne 1} \right) \cr&\Leftrightarrow {1 \over {|x + 2|}} < {2 \over {|x - 1|}} \cr 
& \Leftrightarrow 2|x + 2| - |x - 1| > 0  \text{     } (1)\cr} \)

Bảng xét dấu:

+) Với \(x <  - 2\) ta có:

\(\begin{array}{l}\left( 1 \right) \Leftrightarrow 2\left( { - x - 2} \right) - \left( { - x + 1} \right) > 0\\ \Leftrightarrow  - 2x - 4 + x - 1 > 0\\ \Leftrightarrow  - x - 5 > 0\\ \Leftrightarrow  - x > 5\\ \Leftrightarrow x <  - 5\end{array}\)

Kết hợp với \(x <  - 2\) ta được \(x <  - 5\).

+) Với \( - 2 < x < 1\) ta có:

\(\begin{array}{l}\left( 1 \right) \Leftrightarrow 2\left( {x + 2} \right) - \left( { - x + 1} \right) > 0\\ \Leftrightarrow 2x + 4 + x - 1 > 0\\ \Leftrightarrow 3x + 3 > 0\\ \Leftrightarrow 3x >  - 3\\ \Leftrightarrow x >  - 1\end{array}\)

Kết hợp với \( - 2 < x < 1\) ta được \( - 1 < x < 1\)

+) Với \(x > 1\) ta có:

\(\begin{array}{l}\left( 1 \right) \Leftrightarrow 2\left( {x + 2} \right) - \left( {x - 1} \right) > 0\\ \Leftrightarrow 2x + 4 - x + 1 > 0\\ \Leftrightarrow x + 5 > 0\\ \Leftrightarrow x >  - 5\end{array}\)

Kết hợp với \(x > 1\) ta được \(x > 1\).

Vậy bất phương trình có nghiệm \(\left[ \begin{array}{l}x <  - 5\\ - 1 < x < 1\\x > 1\end{array} \right.\)

Tập nghiệm của bất phương trình là: \(T = (-∞; - 5) ∪ (- 1; 1) ∪ (1; +∞)\).

Cách 2:

\(\begin{array}{l}
\dfrac{5}{{\left| {x + 2} \right|}} < \dfrac{{10}}{{\left| {x - 1} \right|}}\\ \left( {DK:x \ne - 2,x \ne 1} \right)\\
\Leftrightarrow \dfrac{1}{{\left| {x + 2} \right|}} < \dfrac{2}{{\left| {x - 1} \right|}}\\
\Rightarrow \left| {x - 1} \right| < 2\left| {x + 2} \right|\\
\Leftrightarrow {\left( {x - 1} \right)^2} < 4{\left( {x + 2} \right)^2}\\
\Leftrightarrow {x^2} - 2x + 1 < 4\left( {{x^2} + 4x + 4} \right)\\
\Leftrightarrow 3{x^2} + 18x + 15 > 0\\
\Leftrightarrow 3\left( {x + 1} \right)\left( {x + 5} \right) > 0
\end{array}\)

Ta có bảng xét dấu:

Xét dấu ta được \(\left[ \begin{array}{l}x < - 5\\x > - 1\end{array} \right.\)

Kết hợp điều kiện \(x\ne -2,x\ne 1\) ta được tập nghiệm của bất phương trình là: \(T = (-∞; - 5) ∪ (- 1; 1) ∪ (1; +∞)\).

HocTot.Nam.Name.Vn