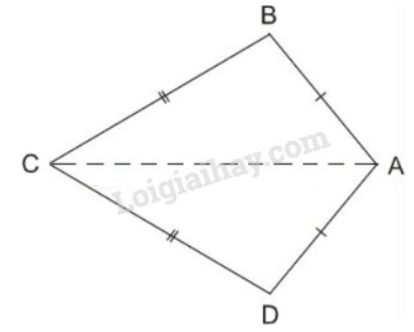
Bài 3 trang 67 SGK Toán 8 tập 1

LG a.

Chứng minh rằng \(AC\) là đường trung trực của \(BD.\)

Phương pháp giải:

Áp dụng: Tính chất: Một điểm thuộc đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.

Lời giải chi tiết:

Ta có: \(AB = AD\) (giả thiết) \( \Rightarrow  A\) thuộc đường trung trực của \(BD\) (Theo tính chất một điểm cách đều hai đầu của đoạn thẳng thì thuộc đường trung trực của đoạn thẳng đó).

\(CB = CD\) (giả thiết) \( \Rightarrow  C\) thuộc đường trung trực của \(BD\) (Theo tính chất một điểm cách đều hai đầu của đoạn thẳng thì thuộc đường trung trực của đoạn thẳng đó).

Vậy \(AC\) là đường trung trực của \(BD.\)

LG b.

Tính \(\widehat B;\widehat D\) biết rằng \(\widehat A = {100^0};\widehat C = {60^0}\).

Phương pháp giải:

Áp dụng:

- Định lý: Tổng các góc của một tứ giác bằng \({360^0}\)

- Tính chất hai tam giác bằng nhau.

Lời giải chi tiết:

Xét \(∆ ABC\) và \(∆ADC\) có:

  +) \(AB = AD\) (giả thiết)

  +) \(BC = DC\) (giả thiết)  

  +) \(AC\) cạnh chung

Suy ra \(∆ ABC = ∆ADC\) (c.c.c)  

\(\Rightarrow \widehat B = \widehat D\) (hai góc tương ứng)

Xét tứ giác \(ABCD\), ta có: \(\widehat B + \widehat {BC{\rm{D}}} + \widehat {\rm{D}} + \widehat {BA{\rm{D}}} = {360^0}\) (Định lí tổng các góc của một tứ giác).

\(\begin{array}{l}
\Rightarrow \widehat B + \widehat {\rm{D}} = {360^0} - \left( {\widehat {BC{\rm{D}}} + \widehat {BA{\rm{D}}}} \right) \\\;\;\;\;\;\;\;\;\;\;\;= {360^0} - \left( {{{60}^0} + {{100}^0}} \right) = {200^0}\\ \text{Mà  }\widehat B= \widehat D\text{ (chứng minh trên) }\\
\Rightarrow \widehat B+\widehat B = {200^0}\\\Rightarrow 2\widehat B = 200^0
\end{array}\)

 Do đó \(\widehat B = \widehat {\rm{D}} = {200^0}:2 = {100^0}.\)