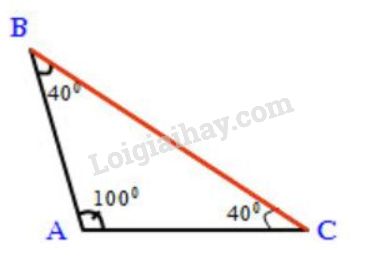
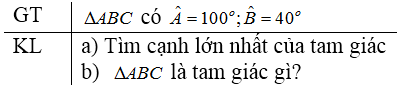Bài 3 trang 56 SGK Toán 7 tập 2Cho tam giác ABC Đề bài Cho tam giác ABCABC với ˆA=100oˆA=100o , ˆB=40oˆB=40o a) Tìm cạnh lớn nhất của tam giác. b) Tam giác ABCABC là tam giác gì? Video hướng dẫn giải Phương pháp giải - Xem chi tiết Áp dụng: - Định lí tổng ba góc trong tam giác bằng 18001800. - Định lí về mối quan hệ giữa góc và cạnh đối diện. Lời giải chi tiết a) Tam giác ABCABC có ˆA=100oˆA=100o và ˆB=40oˆB=40o Áp dụng định lí tổng ba góc trong tam giác vào tam giác ABCABC ta được: ˆA+ˆB+ˆC=1800⇒ˆC=1800−(ˆA+ˆB)=1800−(1000+400)=400 ⇒ˆA>ˆB=ˆC (100o>40o) Vậy ˆA lớn nhất do đó cạnh đối diện với góc A là cạnh BC lớn nhất (Theo định lí về quan hệ giữa góc và cạnh đối diện)
b) Tam giác ABC có ˆC=ˆB=400 do đó ΔABC là tam giác cân tại A HocTot.Nam.Name.Vn
|