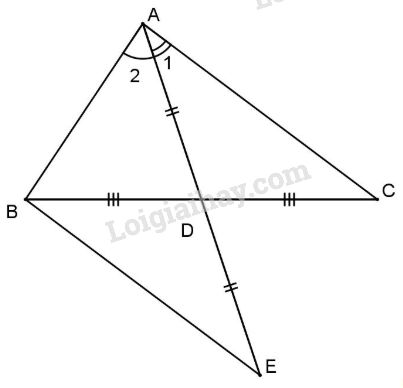
Đề kiểm tra 15 phút - Đề số 1 - Bài 1 - Chương 3 – Hình học 7Giải Đề kiểm tra 15 phút - Đề số 1 - Bài 1 - Chương 3 – Hình học 7 Đề bài Cho tam giác ABC có \(AB < AC\). Gọi D là trung điểm của BC. Trên tia đối của tia DA đặt \(DE=DA\), nối B với E. Chứng minh rằng: a) \(\Delta EDB = \Delta ADC\); b) \(\widehat {BA{\rm{D}}} > \widehat {DAC}\). Phương pháp giải - Xem chi tiết Trong 1 tam giác, góc đồi diện với cạnh lớn hơn thì lớn hơn Lời giải chi tiết
a) Xét \(\Delta E{\rm{D}}B\) và \(\Delta A{\rm{D}}C\) có: +) \(DB = DC\) (gt) +) \(\widehat {B{\rm{D}}E} = \widehat {C{\rm{D}}A}\) (đối đỉnh) +) \(DE = DA\) (gt) Do đó \(\Delta E{\rm{D}}B = \Delta A{\rm{D}}C\) (c.g.c). b) \(\Delta {\rm E}{\rm{D}}B = \Delta A{\rm{D}}C\) (cmt) \( \Rightarrow {\widehat A_1} = \widehat E\) ( 2 góc tương ứng) Mà \(AB < AC\) (gt) \( \Rightarrow AB < BE\) (1) Xét \(\Delta ABE\) có \( AB < BE\) \( \Rightarrow \widehat E < {\widehat A_2}\) ( Trong một tam giác, góc đối diện với cạnh lớn hơn thì lớn hơn) Mà \(\widehat E = {\widehat A_1}\) (cmt). Do đó \({\widehat A_2} > {\widehat A_1}\) hay \(\widehat {BA{\rm{D}}} > \widehat {DAC}\).
|