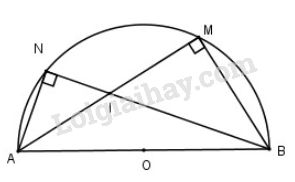
Bài 3 trang 45 SGK Hình học 10

LG a

Chứng minh $\overrightarrow {AI} .\overrightarrow {AM}  = \overrightarrow {AI} .\overrightarrow {AB}$ và $\overrightarrow {BI} .\overrightarrow {BN}  = \overrightarrow {BI} .\overrightarrow {BA}$;

Phương pháp giải:

Sử dụng quy tắc ba điểm, xen điểm thích hợp và chú ý:  $$\overrightarrow a  \bot \overrightarrow b  \Leftrightarrow \overrightarrow a .\overrightarrow b  = 0$$

Lời giải chi tiết:

AB là đường kính nên $\widehat {AMB} = \widehat {ANB} = {90^0}$ (góc nội tiếp chắn nửa đường tròn)

$\Rightarrow \left\{ \begin{array}{l} AM \bot MB\\ AN \bot NB \end{array} \right.$

Ta có: ${\overrightarrow {AI} .\overrightarrow {AM} } = \overrightarrow {AI} \left( {\overrightarrow {AB}  + \overrightarrow {BM} } \right)$

$= \overrightarrow {AI} .\overrightarrow {AB}  + \overrightarrow {AI} .\overrightarrow {BM}$

Mặt khác: $\overrightarrow {AI}  \bot \overrightarrow {BM}$ (do AM$\bot$ MB) nên $\overrightarrow {AI} .\overrightarrow {BM}  = 0$ 

Từ đó: $\overrightarrow {AI} .\overrightarrow {AM}  = \overrightarrow {AI} .\overrightarrow {AB}+0$ $= \overrightarrow {AI} .\overrightarrow {AB}$

Ta có: $\overrightarrow {BI} .\overrightarrow {BN}  = \overrightarrow {BI} \left( {\overrightarrow {BA}  + \overrightarrow {AN} } \right)$$= \overrightarrow {BI} .\overrightarrow {BA}  + \overrightarrow {BI} .\overrightarrow {AN}$

Mặt khác: $\overrightarrow {BI}  \bot \overrightarrow {AN}$ (vì BN $\bot$ NA) nên $\overrightarrow {BI} .\overrightarrow {AN}  = 0$

Từ đó: $\overrightarrow {BI} .\overrightarrow {BN}  =  \overrightarrow {BI} .\overrightarrow {BA}+0$$=\overrightarrow {BI} .\overrightarrow {BA}$.

LG b

 Hãy dùng câu a) để tính $\overrightarrow {AI} .\overrightarrow {AM}  + \overrightarrow {BI} .\overrightarrow {BN}$ theo $R.$

Phương pháp giải:

Sử dụng kết quả câu a suy ra đáp án, chú ý  $$\overrightarrow a .\overrightarrow a  = {\left| {\overrightarrow a } \right|^2}$$

Lời giải chi tiết:

$\eqalign{& \overrightarrow {AI} .\overrightarrow {AM} + \overrightarrow {BI} .\overrightarrow {BN}\cr& = \overrightarrow {AI} .\overrightarrow {AB} + \overrightarrow {BI} .\overrightarrow {BA} \cr & = \overrightarrow {AI} .\overrightarrow {AB}  + \overrightarrow {BI} .\left( { - \overrightarrow {AB} } \right)\cr & = \overrightarrow {AI} .\overrightarrow {AB} - \overrightarrow {BI} .\overrightarrow {AB} \cr&= \overrightarrow {AB} \left( {\overrightarrow {AI} - \overrightarrow {BI} } \right) \cr &  = \overrightarrow {AB} .\left( {\overrightarrow {AI}  + \overrightarrow {IB} } \right)\cr &= \overrightarrow {AB} .\overrightarrow {AB} = {\overrightarrow {AB} ^2} = 4{{\rm{R}}^2} \cr}$

HocTot.Nam.Name.Vn