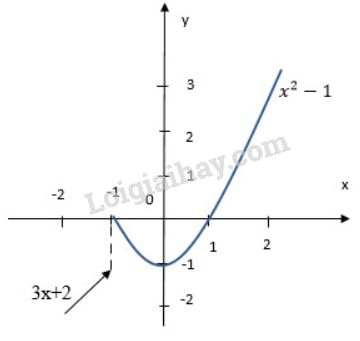
Bài 3 trang 141 SGK Đại số và Giải tích 11

LG a

Vẽ đồ thị của hàm số \(y = f(x)\). Từ đó nêu nhận xét về tính liên tục của hàm số trên tập xác định của nó.

Phương pháp giải:

Khi \(x<-1\), vẽ đường thẳng \(y=3x+2\).

    Khi \(x \ge -1\), vẽ parabol \(y=x^2-1\).

Lưu ý: Vẽ trên cùng một hệ trục tọa độ.

Nhận xét về tính liên tục của hàm số (Đồ thị hàm số có bị gãy khúc tại điểm nào không?)

Lời giải chi tiết:

Khi \(x<-1\), đồ thị hàm số là đường thẳng \(y=3x+2\), khi \( x \ge -1\) đồ thị hàm số là parabol \(y=x^2-1\).

Đồ thị hàm số \(y = f(x)\) là một đường không liền nét mà bị đứt quãng tại \(x_0= -1\). Vậy hàm số đã cho liên tục trên khoảng \((-∞; -1)\) và \((- 1; +∞)\).

LG b

Khẳng định nhận xét trên bằng một chứng minh.

Phương pháp giải:

Hàm số \(y=f(x)\) liên tục tại điểm \(x_0\) \(\Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)

Lời giải chi tiết:

+) Nếu \(x < -1\): \(f(x) = 3x + 2\) liên tục trên \((-∞; -1)\) (vì đây là hàm đa thức nên liên tục trên tập xác định của nó).

+) Nếu \(x> -1\): \(f(x) = x^2- 1\) liên tục trên \((-1; +∞)\) (vì đây là hàm đa thức nên liên tục trên tập xác định của nó).

+) Xét tính liên tục của hàm số tại \(x = -1\);

Ta có 

\(\underset{x\rightarrow -1^{-}}{\lim} f(x) = \)\(\underset{x\rightarrow -1^{-}}{\lim} (3x + 2) = 3(-1) +2 = -1\).

\(\underset{x\rightarrow -1^{+}}{\lim} f(x) = \underset{x\rightarrow -1^{+}}{\lim} (x^2- 1)\)\( = (-1)^2- 1 = 0\).

Vì \(\underset{x\rightarrow -1^{-}}{\lim} f(x) ≠ \underset{x\rightarrow -1^{+}}{\lim} f(x)\) nên không tồn tại \(\underset{x\rightarrow -1}{\lim} f(x)\).

Vậy hàm số gián đoạn tại \(x_0= -1\).

HocTot.Nam.Name.Vn