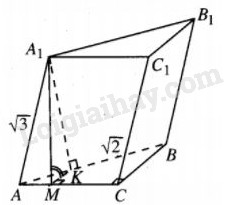
Bài 29 trang 9 SBT Hình học 12 Nâng cao

Đề bài

Cho khối lăng trụ ABC.A₁B₁C₁ có đáy ABC là tam giác vuông cân với cạnh huyền AB bằng \(\sqrt 2 \). Cho biết mặt phẳng \(\left( {A{A_1}B} \right)\) vuông góc với mặt phẳng \(\left( {ABC} \right)\),\({\rm{A}}{{\rm{A}}_1} = \sqrt 3 \), góc \(\widehat {{A_1}AB}\) nhọn , góc giữa mặt phẳng \(\left( {{A_1}AC} \right)\) và mặt phẳng \(\left( {ABC} \right)\) bằng 60⁰. Hãy tính thể tích khối lăng trụ.

Lời giải chi tiết

Hạ \({A_1}K \bot AB\) ( với \(K \in AB)\) thì \({A_1}K \bot \left( {ABC} \right)\). Vì \(\widehat {{A_1}AB}\) nhọn nên K thuộc tia AB.

Kẻ \(KM \bot AC\) thì \({A_1}M \bot AC\) (định lí ba đường vuông góc ), do đó \(\widehat {{A_1}MK}\) = 60⁰,

Giả sử \({A_1}K = x\), ta có :

\(\eqalign{  & AK = \sqrt {{A_1}{A^2} - {A_1}{K^2}}  = \sqrt {3 - {x^2}}  \cr} \)

\(MK = AK.\sin \widehat {KAM}\)

\(=\sqrt {3 - {x^2}} .\sin {45^0} = {{\sqrt 2 } \over 2}\sqrt {3 - {x^2}} .\)

Mặt khác, \(MK = {A_1}K.\cot {60^0} = {x \over {\sqrt 3 }},\) suy ra

\( {{\sqrt{2.\left( {3 - {x^2}} \right)} \over {2}}}  = {x \over {\sqrt 3 }} \Rightarrow x = {3 \over {\sqrt 5 }}.\)

Vậy \({V_{ABC.{A_1}{B_1}{C_1}}} = {S_{ABC}}.{A_1}K \)

\(= {1 \over 2}AC.CB.{A_1}K = {{3\sqrt 5 } \over {10}}\)

HocTot.Nam.Name.Vn