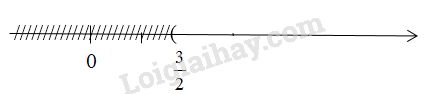
Bài 23 trang 47 SGK Toán 8 tập 2Giải các bất phương trình và biểu diễn tập nghiệm trên trục số: Video hướng dẫn giải Giải các bất phương trình và biểu diễn tập nghiệm trên trục số: LG a. \(2x - 3 > 0\); Phương pháp giải: Áp dụng - Qui tắc chuyển vế Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta đổi dấu hạng tử đó. - Quy tắc nhân với một số Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải: + Giữ nguyên chiều bất phương trình nếu số đó dương. + Đổi chiều bất phương trình nếu số đó âm. Lời giải chi tiết: \(\eqalign{& \,\,2x - 3 > 0 \cr & \Leftrightarrow 2x > 3 \cr & \Leftrightarrow x > {3 \over 2} \cr} \) Vậy tập nghiệm của bất phương trình là: \(S = \left\{ {x\,|\,x > \dfrac{3}{2}} \right\}\) Biểu diễn tập nghiệm trên trục số:
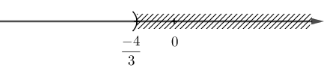
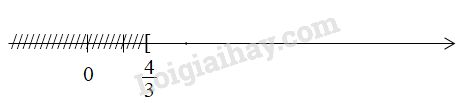
LG b. \(3x + 4 < 0\); Phương pháp giải: Áp dụng - Qui tắc chuyển vế Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta đổi dấu hạng tử đó. - Quy tắc nhân với một số Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải: + Giữ nguyên chiều bất phương trình nếu số đó dương. + Đổi chiều bất phương trình nếu số đó âm. Lời giải chi tiết: \(\eqalign{ Vậy tập nghiệm của bất phương trình là: \(S = \left\{ {x\,|\,x < \dfrac{{ - 4}}{3}} \right\}\) Biểu diễn tập nghiệm trên trục số: LG c. \(4 - 3x ≤ 0\); Phương pháp giải: Áp dụng - Qui tắc chuyển vế Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta đổi dấu hạng tử đó. - Quy tắc nhân với một số Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải: + Giữ nguyên chiều bất phương trình nếu số đó dương. + Đổi chiều bất phương trình nếu số đó âm. Lời giải chi tiết: \(\eqalign{ Vậy tập nghiệm của bất phương trình là: \(S = \left\{ {x\,|\,x \geqslant \dfrac{4}{3}} \right\}\) Biểu diễn tập nghiệm trên trục số:
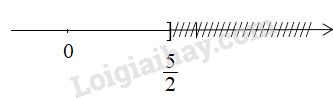
LG d. \(5 - 2x ≥ 0\). Phương pháp giải: Áp dụng - Qui tắc chuyển vế Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta đổi dấu hạng tử đó. - Quy tắc nhân với một số Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải: + Giữ nguyên chiều bất phương trình nếu số đó dương. + Đổi chiều bất phương trình nếu số đó âm. Lời giải chi tiết: \(\eqalign{ Vậy tập nghiệm của bất phương trình là: \(S = \left\{ {x\,|\,x \leqslant \dfrac{5}{2}} \right\}\) Biểu diễn tập nghiệm trên trục số:
HocTot.Nam.Name.Vn
|