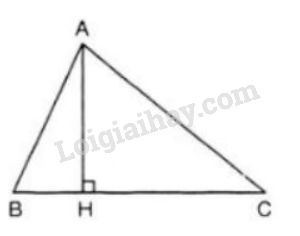
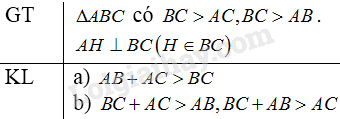Bài 20 trang 64 SGK Toán 7 tập 2

Đề bài

Một cách chứng minh khác của bất đẳng thức tam giác:

Cho tam giác $ABC$. Giả sử $BC$ là cạnh lớn nhất. Kẻ đường vuông góc $AH$ đến đường thẳng $BC$ ($H  \in  BC$).

a) Dùng nhận xét về cạnh lớn nhất trong tam giác vuông ở bài 1 để chứng minh $AB + AC > BC.$

b) Từ giả thiết về cạnh $BC$, hãy suy ra hai bất đẳng thức tam giác còn lại.

Lời giải chi tiết

a) $∆ABC$ có cạnh $BC$ lớn nhất nên chân đường vuông góc kẻ từ $A$ phải nằm giữa $B$ và $C$

Hay $H$ nằm giữa $B$ và $C$ $\Rightarrow  HB  + HC = BC$ 

Trong $∆AHC$ vuông tại $H$ ta có: $HC < AC$    (1) (trong tam giác vuông thì cạnh huyền là cạnh lớn nhất)

Trong $∆AHB$ vuông tại $H$ ta có: $HB < AB$    (2) (trong tam giác vuông thì cạnh huyền là cạnh lớn nhất)

Cộng theo vế hai bất đẳng thức (1), (2) ta có:

$HB + HC < AC + AB$

Vì $HB + HC = BC$ nên $BC < AC + AB.$

b) $BC$ là cạnh lớn nhất nên suy ra $AB < BC$ và $AC < BC$

Vì $AB, AC > 0$ nên ta có: $AB < BC + AC; AC < BC + AB$ 

HocTot.Nam.Name.Vn