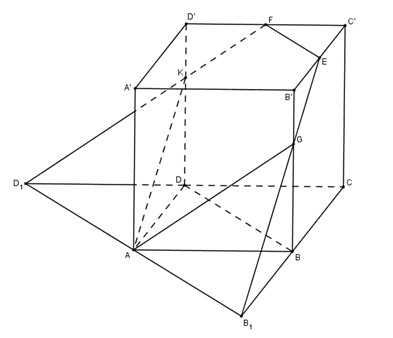
Bài 2 trang 99 SGK Hình học 12Cho khối lập phương ABCD.A'B'C'D' cạnh bằng a. Gọi E và F lần lượt là trung điểm của B'C' và C'D'. Đề bài Cho khối lập phương ABCD.A′B′C′D′ABCD.A′B′C′D′ cạnh bằng aa. Gọi EE và FF lần lượt là trung điểm của B′C′B′C′ và C′D′C′D′. Mặt phẳng (AEF)(AEF) chia khối lập phương đó thành hai khối đa diện (H) và (H') trong đó (H) là khối đa diện chứa đỉnh A′A′. Tính thể tích của (H). Video hướng dẫn giải Phương pháp giải - Xem chi tiết Xác định thiết diện của hình lập phương khi cắt bởi mặt phẳng (AEF). Phân chia và lắp ghép các khối đa diện. Tính thể tích của (H'): V(H′)=VC′EF.CB1D1−VA.BB1D−VDD1KV(H′)=VC′EF.CB1D1−VA.BB1D−VDD1K Lời giải chi tiết
Cách vẽ thiết diện: Ta có EF//B′D′EF//B′D′ mà B′D′//BDB′D′//BD nên từ AA kẻ đường song song với BDBD, cắt CDCD kéo dài tại D1D1 và CBCB kéo dài tại B1B1. Nối B1EB1E cắt BB′BB′ tại GG. Nối D1FD1F cắt DD′DD′ tại KK. Thiết diện là ngũ giác AGEFKAGEFK. Hình (H) là khối AGEFK.A′B′D′AGEFK.A′B′D′. Theo giả thiết EE là trung điểm của B′C′B′C′; FF là trung điểm của C′D′C′D′, ta có BB1=BC=a=2B′EBB1=BC=a=2B′E ⇒BG=2GB′=23a⇒BG=2GB′=23a Từ đó VA.BB1G=13AB.SBB1G=13a.12.a.23a=a39=V1VA.BB1G=13AB.SBB1G=13a.12.a.23a=a39=V1 V(A.DD1K)=13.SΔDD1K.AD=19a3=V2 Ta có: SΔCB1D1=12CB1.CD1=2a2; SΔEC′F=12.C′E.C′F=a28 Chiều cao hình chóp cụt CB1D1.C′EFlà CC′=a VCC1D1.C′EF=13a(2a2+a28+a22)=7a38 Thể tích của khối (H') bằng: V(H′)=VCC1D1.C′EF−(V1+V2)=78a3−29a3=4772a3 Từ đó thể tích của khối (H) bằng: V(H)=Vlập phương−V(H') = a3−4772a3=2572a3 HocTot.Nam.Name.Vn
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
|