Bài 2 trang 66 SGK Toán 8 tập 1

LG a.

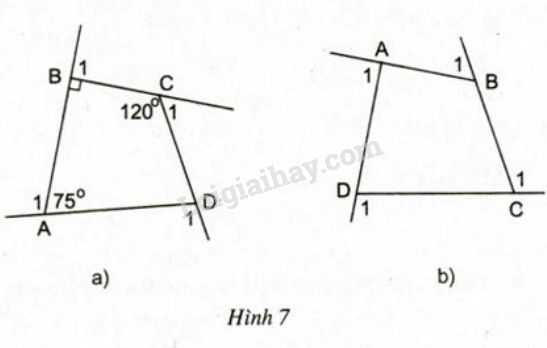
Tính các góc ngoài của tứ giác ở hình 7a.

Phương pháp giải:

Áp dụng định lý: Tổng các góc trong tứ giác bằng \({360^0}\)

Lời giải chi tiết:

\(\widehat A + \widehat B + \widehat C + \widehat D = {360^0}\) (định lý tổng các góc của tứ giác)

\(\begin{array}{l}
\widehat {{D}}= {360^0} - \left( {\widehat A + \widehat B + \widehat C} \right)\\
= {360^0} - \left( {{75}^0+{{90}^0} + {{120}^0}} \right)\\
= {360^0} - {285^0}\\= {75^0}
\end{array}\)

Ta có:

+) \(\widehat {BAD} + \widehat {{A_1}} = {180^0}\) (2 góc kề bù)

\(\begin{array}{l}
\widehat {{A_1}} = {180^0} - \widehat {BAD}\\
= {180^0} - {75^0} = {105^0}.
\end{array}\)

+) \(\widehat {{B_1}} + \widehat {CBA} = {180^0}\) (2 góc kề bù)

\(\begin{array}{l}
\widehat {{B_1}} = {180^0} - \widehat {CBA}\\= {180^0} - {90^0} = {90^0}.
\end{array}\)

+) \(\widehat {{C_1}} + \widehat {BCD} = {180^0}\) (2 góc kề bù)

\(\begin{array}{l}
\widehat {{C_1}} = {180^0} - \widehat {BC{\rm{D}}}\\= {180^0} - {120^0} = {60^0}.
\end{array}\)

+) \(\widehat {{D_1}} + \widehat {ADC} = {180^0}\)

\(\begin{array}{l}
\widehat {{D_1}} = {180^0} - \widehat {{\rm{ADC}}}\\= {180^0} - {75^0} = {105^0}.
\end{array}\)

LG b.

Tính tổng các góc ngoài của tứ giác ở hình 7b (tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài): \(\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = ?\)

Phương pháp giải:

Áp dụng định lý: Tổng các góc trong tứ giác bằng \({360^0}\)

Lời giải chi tiết:

Ta có: 

+) \(\widehat {A} + \widehat {{A_1}} = {180^0}\) (2 góc kề bù) \(\Rightarrow \widehat {{A_1}} = {180^0}-\widehat {A} \)

+) \(\widehat {B} + \widehat {{B_1}} = {180^0}\) (2 góc kề bù) \(\Rightarrow \widehat {{B_1}} = {180^0}-\widehat {B} \)

+) \(\widehat {C} + \widehat {{C_1}} = {180^0}\) (2 góc kề bù) \(\Rightarrow \widehat {{C_1}} = {180^0}-\widehat {C} \)

+) \(\widehat {D} + \widehat {{D_1}} = {180^0}\) (2 góc kề bù) \(\Rightarrow \widehat {{D_1}} = {180^0}-\widehat {D} \)

Lại có: \(\widehat {{A}} + \widehat {{B}} + \widehat {{C}} + \widehat {{D}} = {360^0}\) (định lý tổng 4 góc trong tứ giác ABCD)

Ta có: 

\(\begin{array}{l}
\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}}\\ = \left( {{{180}^0} - \widehat {{A}}} \right) + \left( {{{180}^0} - \widehat {{B}}} \right) \\\;\;\;+ \left( {{{180}^0} - \widehat {{C}}} \right) + \left( {{{180}^0} - \widehat {{D}}} \right)\\
= {180^0}.4 - \left( {\widehat {{A}} + \widehat {{B}} + \widehat {{C}} + \widehat {{D}}} \right)\\
= {720^0} - {360^0} = {360^0}.
\end{array}\)

LG c.

Có nhận xét gì về tổng các góc ngoài của tứ giác?

Phương pháp giải:

Áp dụng tính chất: Tổng hai góc kề bù bằng \({180^0}\)

Lời giải chi tiết:

Nhận xét: Tổng các góc ngoài của tứ giác bằng \({360^0}\) 

HocTot.Nam.Name.Vn