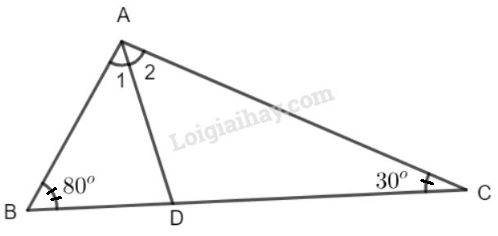
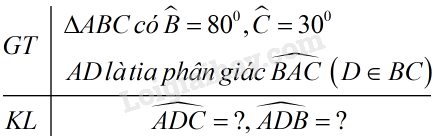Bài 2 trang 108 SGK Toán 7 tập 1

Đề bài

 Cho tam giác $ABC$ có $\widehat{B}= 80^0$, $\widehat{C}=  30^0$. Tia phân giác của góc $A$ cắt $BC$ ở $D$. Tính $\widehat{ADC},\widehat{ADB}$.

Lời giải chi tiết

 

Áp dụng định lí tổng ba góc của một tam giác vào $\Delta ABC$ ta có:

$\widehat {BAC} + \widehat B + \widehat C = {180^0}$

$\widehat{BAC}= 180^0- (\widehat{B}+\widehat{C})$ $= 180^0-( 80^0+ 30^0)= 70^0$ 

Vì $AD$ là tia phân giác của $\widehat{BAC}$ nên $\widehat{A_{1}}=\widehat{A_{2}}=\dfrac{\widehat{BAC}}2=\dfrac{70^{0}}2= 35^0$

Vì $\widehat{ADC}$ là góc ngoài tại đỉnh $D$ của $\Delta ABD$ nên

$\widehat{ADC} = \widehat{B} + \widehat{A_{1}}$ (góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó)  

$\Rightarrow \widehat {ADC}=80^0+ 35^0= 115^0$

$\widehat{ADC}$ và $\widehat{ADB}$ là hai góc kề bù 

Do đó $\widehat{ADB}+ \widehat{ADC}=  180^0$

$\Rightarrow \widehat{ADB}=  180^0- \widehat{ADC}= 180^0-115^0$$=65^0$

Vậy $\widehat {ADC}= 115^0;$$\widehat {ADB}= 65^0;$

HocTot.Nam.Name.Vn