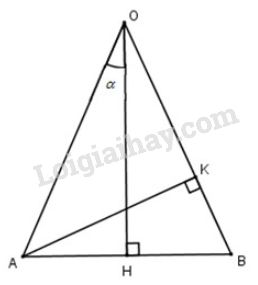
Bài 2 trang 40 SGK Hình học 10Cho AOB là tam giác cân tại O có OA = a và có các đường cao OH và AK. Đề bài Cho AOBAOB là tam giác cân tại OO có OA=aOA=a và có các đường cao OHOH và AK.AK. Giả sử ^AOH=α.ˆAOH=α. Tính AKAK và OKOK theo aa và α.α. Video hướng dẫn giải Phương pháp giải - Xem chi tiết +) Sử dụng công thức lượng giác đối với góc nhọn ta có: sinα=cạnhđốicạnhhuyền và cosα=cạnhkềcạnhhuyền Lời giải chi tiết
TH1: α<450 Do tam giác OAB cân tại O nên ta có ^AOB=2^AOH=2α<900 Tam giác OKA vuông tại K nên ta có: sin^AOK=AKOA ⇒AK=OA.sin^AOK⇒AK=a.sin2α. cos^AOK=OKOA ⇒OK=OA.cos^AOK⇒OK=a.cos2α. TH2: α>450 Do tam giác OAB cân tại O nên ta có ^AOB=2^AOH=2α>900
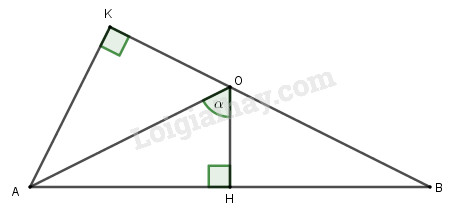
Tam giác AKO vuông tại K có AO=a, ^AOK=1800−^AOB=1800−2α Khi đó: sin^AOK=AKOA⇒AK=OAsin^AOK=asin(1800−2α)=asin2αcos^AOK=OKOA⇒OK=OAcos^AOK=acos(1800−2α)=−acos2α HocTot.Nam.Name.Vn
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
|