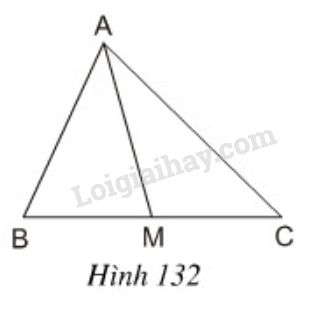
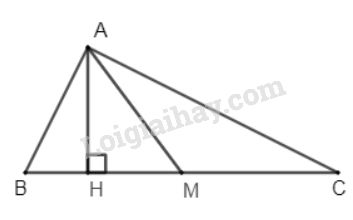
Bài 18 trang 121 SGK Toán 8 tập 1Cho tam giác ABC và đường trung tuyến AM(h. 132). Chứng minh rằng: Đề bài Cho tam giác \(ABC\) và đường trung tuyến \(AM\) (h.\(132\)). Chứng minh rằng: \({S_{AMB}} = {S_{AMC}}\) Video hướng dẫn giải Phương pháp giải - Xem chi tiết - Dựng \(AH\) là đường cao của \(\Delta ABC\). - Áp dụng công thức tính diện tích tam giác. Lời giải chi tiết
Dựng \(AH\) là đường cao của \(\Delta ABC\), khi đó \(\Delta ABM,\Delta AMC\) có chung chiều cao \(AH\). Ta có: \({S_{AMB}} = \dfrac{1}{2}BM.AH\) (chiều cao \(AH\) và cạnh đáy \(BM\)) \({S_{AMC}} = \dfrac{1}{2}CM.AH\) (chiều cao \(AH\) và cạnh đáy \(CM\)) Mà \(BM = CM\) (vì \(AM\) là đường trung tuyến) Vậy \({S_{AMB}} = {S_{AMC}}.\) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
