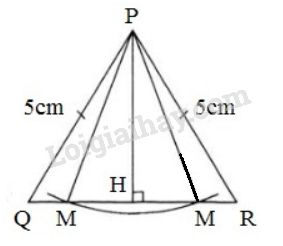
Bài 14 trang 60 SGK Toán 7 tập 2

Đề bài

Đố : Vẽ tam giác $PQR$ có $PQ = PR =5\,cm$, $QR = 6\,cm$. Lấy điểm $M$ trên đường thẳng $QR$ sao cho $PM = 4,5\,cm$. Có mấy điểm $M$ như vậy ?

Điểm $M$ có nằm trên cạnh $QR$ hay không ? Tại sao ?

Lời giải chi tiết

* Vẽ hình:

- Vẽ tam giác $PQR$ có $PQ = PR = 5\,cm,\; QR = 6\,cm$.

+ Vẽ đoạn thẳng $QR = 6\,cm$.

+ Vẽ cung tròn tâm $Q$ và cung tròn tâm $R$ bán kính $5\,cm$. Hai cung tròn này cắt nhau tại $P$.

+ Nối $PQ$ và $PR$ ta được tam giác cần vẽ.

- Vẽ điểm $M$: Vẽ cung tròn tâm $P$ bán kính $4,5\,cm$ cắt đường thẳng $QR$ (nếu có) tại $M$.

* Chứng minh 

$∆PQR$ có $PQ = PR = 5\,cm$ nên $∆PQR$ cân tại $P$. Từ $P$ kẻ đường thẳng $PH ⊥ QR$.

Xét hai tam giác vuông tại H: $ΔPHQ$ và $ΔPHR$ có

$PH$ chung

$PQ = PR ( = 5cm)$

$⇒ ΔPHQ = ΔPHR$ (cạnh huyền – cạnh góc vuông)

$⇒ HQ = HR$ (Hai cạnh tương ứng)

Mà $HQ + HR = QR = 6 cm$

Suy ra $HQ=HR=QR:2=6:2=3cm$

+ $ΔPHR$ vuông tại H có $PR^2= PH^2+ HR^2$ (định lí Py – ta – go)

$⇒ PH^2= PR^2– HR^2= 5^2– 3^2= 16$$⇒ PH = 4cm .$

Đường vuông góc $PH = 4cm$ là đường ngắn nhất trong các đường kẻ P đến đường thẳng QR.

Vậy chắc chắn có đường xiên $PM = 4,5cm$ (vì $PM = 4,5cm > 4cm)$ kẻ từ P đến đường thẳng QR.

Gọi $M$ là một điểm nằm trên đường thẳng $QR$.

Ta có: $MH, QH, RH$ lần lượt là hình chiếu của $PM, PQ, PR$ trên $QR$.

Vì $PM = 4,5\,cm < PQ$ (hoặc $PR$) nên $MH < QH, MH < RH$.

- Tương tự trên $RH$ có $MH < RH$ nên $M$ nằm giữa hai điểm $R$ và $H$.

Do vậy có hai điểm $M$ thỏa mãn điều kiện đề bài và điểm $M$ này nằm trên cạnh $QR$.

HocTot.Nam.Name.Vn