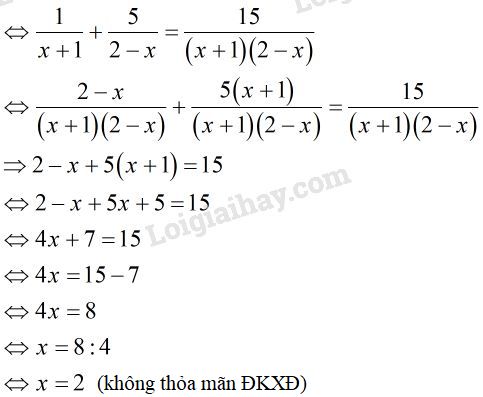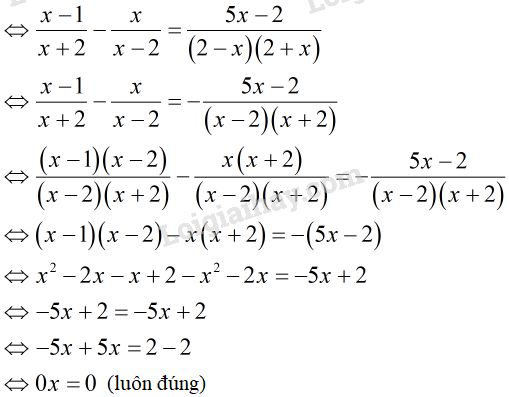Bài 10 trang 131 SGK Toán 8 tập 2Giải các phương trình: Video hướng dẫn giải Giải các phương trình: LG a. \(\dfrac{1}{{x + 1}} - \dfrac{5}{{x - 2}} = \dfrac{{15}}{{\left( {x + 1} \right)\left( {2 - x} \right)}}\) Phương pháp giải: - Tìm điều kiện xác định. - Qui đồng khử mẫu. - Rút gọn rồi tìm nghiệm \(x\). - Đối chiếu với điều kiện xác định rồi kết luận nghiệm. Lời giải chi tiết: \(\dfrac{1}{{x + 1}} - \dfrac{5}{{x - 2}} = \dfrac{{15}}{{\left( {x + 1} \right)\left( {2 - x} \right)}}\) ĐKXĐ: \(x \ne - 1;x \ne 2\)
Vậy phương trình vô nghiệm. LG b. \(\dfrac{{x - 1}}{{x + 2}} - \dfrac{x}{{x - 2}} = \dfrac{{5x - 2}}{{4 - {x^2}}}\) Phương pháp giải: - Tìm điều kiện xác định. - Qui đồng khử mẫu. - Rút gọn rồi tìm nghiệm \(x\). - Đối chiếu với điều kiện xác định rồi kết luận nghiệm. Lời giải chi tiết: \(\dfrac{{x - 1}}{{x + 2}} - \dfrac{x}{{x - 2}} = \dfrac{{5x - 2}}{{4 - {x^2}}}\) ĐKXĐ:\(x \ne \pm 2\)
Vậy phương trình nghiệm đúng với mọi \(x \ne \pm 2\) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
