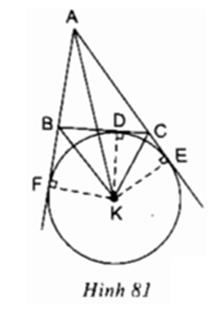
Trả lời câu hỏi 4 Bài 6 trang 115 SGK Toán 9 Tập 1Cho tam giác ABC, K là giao điểm các đường phân giác của hai góc ngoài tại B và C; D, E, F Đề bài Cho tam giác ABC, K là giao điểm các đường phân giác của hai góc ngoài tại B và C; D, E, F theo thứ tự là chân các đường vuông góc kẻ từ K đến các đường thẳng BC, AC, AB (h.81). Chứng minh rằng ba điểm D, E, F năm trên cùng một đường tròn có tâm K.
Video hướng dẫn giải Phương pháp giải - Xem chi tiết Sử dụng tính chất tia phân giác: "Các điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó". Lời giải chi tiết Theo tính chất tia phân giác, ta có: AK là tia phân giác của góc BAC \( \Rightarrow KE{\rm{ }} = {\rm{ }}KF\) Tương tự: CK là tia phân giác của góc ngoài của góc ACB \( \Rightarrow KE{\rm{ }} = {\rm{ }}KD\) Do đó: KE = KF = KD Vậy 3 điểm D, E, F cùng nằm trên đường tròn tâm K.
|