Nội dung từ Loigiaihay.Com
Số thập phân là gì? Cách chuyển phân số, hỗn số thành số thập phân - Toán 5
1. Số thập phân là gì?
2. Cấu tạo số thập phân
3. Hàng của số thập phân. Đọc, viết số thập phân
4. Chuyển các phân số, hỗn số thành số thập phân
5. Bài tập vận dụng
1. Số thập phân là gì?
Các phân số thập phân 110 ; 1100 ; 11000 được viết thành 0,1 ; 0,01 ; 0,001
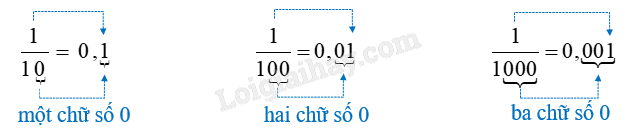
Các số 0,1; 0,01; 0,001 được gọi là số thập phân.
Tương tự ta có:
310=0,3;5100=0,05
5110=5,1;3191000=3,019
Các số 0,3 ; 0,5 ; 5,1 ; 3,019 ; ... là các số thập phân.
2. Cấu tạo số thập phân
- Mỗi số thập phân gồm hai phần: phần nguyên và phần thập phân, chúng được phân cách bởi dấu phẩy.
- Những chữ số ở bên trái dấu phẩy thuộc về phần nguyên, những chữ số ở bên phải dấu phẩy thuộc về phần thập phân

3. Hàng của số thập phân. Đọc, viết số thập phân
Ví dụ:
- Số gồm 2 đơn vị, 3 phần mười, 1 phần trăm, 5 phần nghìn
Viết là: 2,315 ; Đọc là: Hai phẩy ba trăm mười lăm
- Số gồm 0 đơn vị, 2 phần mười, 7 phần trăm, 9 phần nghìn
Viết là: 0,279 ; Đọc là: Không phẩy hai trăm bảy mươi chín
|
· Muốn viết một số thập phân, trước hết viết phần nguyên, viết dấu phẩy, sau đó viết phần thập phân. · Muốn đọc một số thập phân, trước hết đọc phần nguyên, đọc dấu phẩy, sau đó đọc phần thập phân. |
4. Chuyển các phân số, hỗn số thành số thập phân
– Nếu phân số đã cho chưa là phân số thập phân thì ta chuyển các phân số thành phân số thập phân.
– Đếm xem mẫu số có bao nhiêu chữ số 0, thì dịch chuyển dấu phẩy về bên trái bấy nhiêu chữ số.
Ví dụ 1: Chuyển các phân số sau thành số thập phân
810 151000 325 7125
Cách giải
810=0,8 151000=0,015
325=3×425×4=12100=0,12 7125=7×8125×8=561000=0,056
Ví dụ 2: Viết các hỗn số sau thành số thập phân
2310 521100
245 134
Cách giải
2310=2,3 521100=5,21
245=2810=2,8 134=175100=1,75













