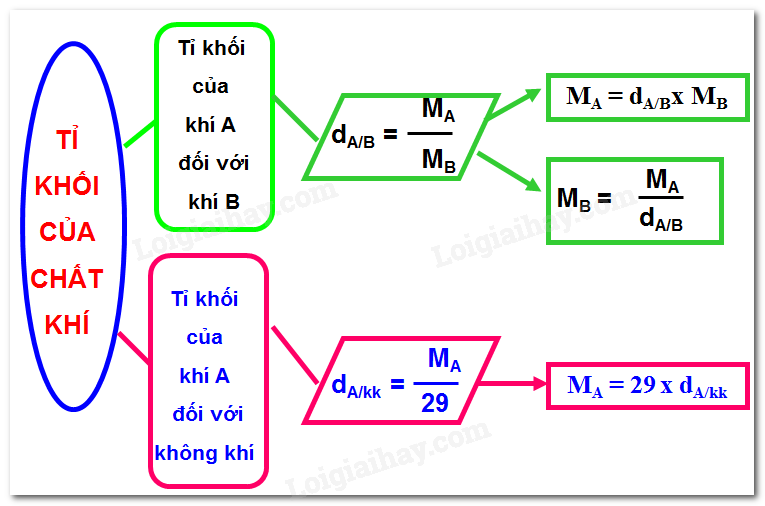
Phương pháp giải một số bài tập tính tỉ khối của chất khí

Dạng 1: Tính tỉ khối của chất khí

* Một số lưu ý cần nhớ:

- Khí A đối với khí B: 

d_A/B = \(\dfrac{M_{A}}{M_{B}}\)

- Khí A đối với không khí: 

d_A/kk = \(\dfrac{M_{A}}{29}\)

* Một số ví dụ điển hình:

Ví dụ 1: Tỉ khối của khí B đối với oxi là 0,5 và tỉ khối của khí A đối với khí B là 2,125. Khối lượng mol của khí A là

Hướng dẫn giải chi tiết:

Ta có: \({d_{B/{O_2}}} = \frac{{{M_B}}}{{{M_{{O_2}}}}} = 0,5 = > {M_B} = 32.0,5 = 16\) 

Mặt khác: \({d_{A/B}} = \frac{{{M_A}}}{{{M_B}}} = 2,125 = > {M_A} = 2,125.16 = 34\)

Vậy khối lượng mol của A là 34 g/mol

Ví dụ 2: Một khí X₂ có tỉ khối hơi đối với khí axetilen (C₂H₂) bằng 2,731. Khí X₂ là

Hướng dẫn giải chi tiết:

Áp dụng công thức tính tỉ khối:  

\({d_{{X_2}/{C_2}{H_2}}} = \frac{{{M_{{X_2}}}}}{{{M_{{C_2}{H_2}}}}} = 2,731 = > {M_{{X_2}}} = (12.2 + 2).2,731 \approx 71\)

Mà = 2.M_X = 71 => M_X = 35,5

Vậy khí cần tìm là Cl₂

Ví dụ 3: Khí A có công thức phân tử dạng RO₂, có tỉ khối hơi so với H₂ là 32. Vậy A có công thức phân tử là:

Hướng dẫn giải chi tiết:

Khí A có tỉ khối so với H₂ là 32

\({d_{A/{H_2}}} = \frac{{{M_A}}}{{{M_{{H_2}}}}} = > {M_A} = {d_{A/{H_2}}}.{M_{{H_2}}} = 32.2 = 64\)

A có công thức phân tử là RO₂ => M = M_R + 2.M_O = 64

=> M_R = 64 – 2.16 = 32 => R là nguyên tố S

Vậy công thức phân tử của A là SO₂

Dạng 2: Xác định tỉ khối của hỗn hợp khí

* Một số lưu ý cần nhớ:

B1: Xác định khối lượng mol trung bình của hỗn hợp khí

B2: Xác định tỉ khối của hỗn hợp khí

* Một số ví dụ điển hình:

Ví dụ 1: Tỉ khối của hỗn hợp chứa N₂ và O₃ theo tỉ lệ 1 : 2 so với không khí là:

Hướng dẫn giải chi tiết:

Gọi số mol của N₂ là a mol => số mol của O₃ là 2a mol

Khối lượng trung bình của hỗn hợp khí là:

\(\bar M = \frac{{{n_{{N_2}}}.{M_{{N_2}}} + {n_{{O_3}}}.{M_{{O_3}}}}}{{{n_{{N_2}}} + {n_{{O_3}}}}} = \frac{{a.28 + 2{\text{a}}.48}}{{a + 2{\text{a}}}} = \frac{{124}}{3}\)

=> tỉ khối của hỗn hợp so với không khí là:  

\({d_{hh/kk}} = \frac{{\bar M}}{{{M_{kk}}}} = \frac{{124}}{{3.29}} = \frac{{124}}{{87}}\)

Ví dụ 2: Tỉ khối của hỗn hợp chứa 4 gam metan (CH₄) và 7 gam khí etilen (C₂H₄) so với không khí là:

Hướng dẫn giải chi tiết:

Số mol của CH₄ là:  

\({n_{C{H_4}}} = \frac{4}{{16}} = 0,25\,mol\)

Số mol của C₂H₄ là: 

\({n_{{C_2}{H_4}}} = \frac{7}{{28}} = 0,25\,mol\)

=> khối lượng trung bình của hỗn hợp khí là:

\(\bar M = \frac{{{n_{C{H_4}}}.{M_{C{H_4}}} + {n_{{C_2}{H_4}}}.{M_{{C_2}{H_4}}}}}{{{n_{C{H_4}}} + {n_{{C_2}{H_4}}}}} = \frac{{{m_{C{H_4}}} + {m_{{C_2}{H_4}}}}}{{{n_{C{H_4}}} + {n_{{C_2}{H_4}}}}} = \frac{{4 + 7}}{{0,25 + 0,25}} = 22\)

=> tỉ khối của hỗn hợp so với không khí là:  

\({d_{hh/kk}} = \frac{{\bar M}}{{{M_{kk}}}} = \frac{{22}}{{29}}\)

Ví dụ 3: Một hỗn hợp X gồm H₂ và O₂ (không có phản ứng xảy ra) có tỉ khối so với không khí là 0,3276. Phần trăm theo số mol của khí H₂ trong hỗn hợp là

Hướng dẫn giải chi tiết:

Gọi số mol của H₂ và O₂ trong hỗn hợp lần lượt là x và y mol

Tỉ khối của X so với không khí :  

\({d_{X/kk}} = \dfrac{{{{\bar M}_X}}}{{29}} = > {\bar M_X} = 29.0,3276 = 9,5\)

Công thức tính khối lượng trung bình của hỗn hợp X là

\({M_X} = \dfrac{{{n_{{H_2}}}.{M_{{H_2}}} + {n_{{O_2}}}.{M_{{O_2}}}}}{{{n_{{H_2}}} + {n_{{O_2}}}}} = \dfrac{{2{\text{x}} + 32y}}{{x + y}} = 9,5\)

=> 2x + 32y = 9,5x + 9,5y => 7,5x = 22,5 => x = 3y

=> phần trăm số mol khí H₂ là:  

\(\% {n_{{H_2}}} = \dfrac{{{n_{{H_2}}}}}{{{n_{{H_2}}} + {n_{{O_2}}}}}.100\% = \dfrac{{3y}}{{3y + y}}.100\% = 75\% \)

HocTot.Nam.Name.Vn